円錐の表面積の求め方がわかる3ステップ 円錐の表面積は3ステップで計算できちゃう^_^ つぎの例題をときながらみてみよう。 半径3cm、母線の長さが10cmの円錐の表面積を10秒以内に計算して。 Step1 底面の「円周の長さ」を計算したる まずは底面の「円周半径4cm・高さ6cmの円柱 ※円周率を314とした場合 円の面積=4cm×4cm×314=5024cm 2 円の円周=4cm×2×314=2512cm 側面の面積=6cm×2512cm=cm 2 円柱の面積=5024cm 2 5024cm 2 cm 2 =2512cm 2 ※円周率をπとした場合三角柱の底面積=4×10÷2=cm 2 円錐の底面積 円錐の底面積は、円柱の底面積と同じです。円の面積を求めれば良いですね。下記の通りです。 円錐の底面積=5×5×314=785cm 2 四角錐の底面積 四角錐の底面積は、四角柱の底面積と同じ計算です。

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
円錐 面積
円錐 面積-TypeXH 2. α=βのとき、放物線となることの証明 1)円すいに内接し切断面に接する球を考え、切断面との 交点をFとする。交差線上の任意の位置に点Pをとり 円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ



円錐や角錐の体積 カヴァリエーリの法則 渡邊勝 立命館慶祥高校 部活が終わって 素男と聡子がなにやら話している 素男 円筒の中に円錐 があるとするよ 底面が共通でさ 高さが同じ円錐の体積が円筒の体積三分の一というのがどうもおかしいよ
円錐の表面積 底面の半径が r ,母線の長さが R の円錐の表面積を求めるには,右図のように展開図で考え,底面積=円と側面積=扇形の面積を各々求めて加えるとよい. 底面は半径 r の円だから,その面積は πr 2 (1) 側面の扇形の面積を求めるためには,その中心角を求めることが重要に となります。底面の面積\(\pi R^2\)と高さ\(h\)の積です。 円錐の体積の計算 では円錐の体積を計算します。円柱の場合と違うのは変数\(r\)の積分が\(z\)に束縛されている点です。 そこで\(r\)を\(z\)の関数に変換する必要があります。 母線が\(z\)の関数Keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 1438 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご意見
No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2 2円錐台の体積 拡底部の円錐台状の箇所に入れるコンクリート量を計算しました。 大変使いやすかったです。 植木鉢の土の量を計算するために使わせていただきました。 円錐台の側面積を求めたかったから。 円周率をπと表示できるようになると側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなる
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru$$(底面積)×(高さ)×\frac{1}{3}=(体積)$$ で求められます。~~すいの立体のときは,$$\frac{1}{3}$$をかけ算するのがポイントです。 まず,底面積から求めると,次の図の部分だとわかります。 あとは 高さ が知りたいですよね。図からこの部分だとわかります。 解答π × (r1 r2)× √ ((r1 r2) × (r1 r2) 高さ × 高さ) π × (r1 × r1 r2 × r2)



1




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題
積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。 円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。) 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であることから円錐の側面積 2112 円錐の側面積(展開図にすると扇形の部分)の公式 A=πrl (A面積、r半径、l母線の長さ) は円錐の展開図から簡単に求められますが これを積分で求めようとするとなぜか A=πrh(h円錐の高さ)になってしまい、うまくいきませ




135 I24picm2 Descubre Como Resolverlo En Qanda




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐の側面積の求め方がわかる3ステップ 円錐の側面積は3つのステップでもとめることができるよ。 つぎの例題をといていこう! 例題 半径3cm、母線の長さ10cmの円錐の側面積を求めてくれ! Step1 底面の「円周の長さ」を求める!ですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 × 半径 × π 5 × 3 × π = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 27 立体の体積と表面積 143 右の図の円錐について,次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図の円錐の体積を求めよ。




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
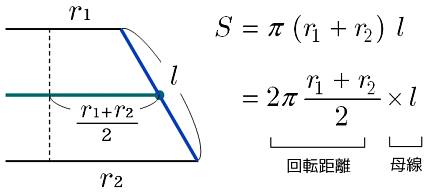



初等幾何 円錐台の側面積を求める 大人が学び直す数学
円錐の側面積の求め方が分かりません。 そのため、以下の公式になります。 クリックして Bing でレビューする1011 円すいの側面積の求め方 — Duration 747 ですが、これを活用しない限りは現状は変わらないです。 14 まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積直円錐(ちょくえんすい) 直円錐とは、底面の円の中心と頂点とを結ぶ線が、底面に垂直である円錐のことです。 図のような母線10cm、半径6cmの直円錐があるとします。 この直円錐の表面積はいくらでしょう? 直円錐を分解 直円錐の底面を外してみました。




高校入試対策数学 円錐に関する対策問題 Pikuu



円錐や角錐の体積 カヴァリエーリの法則 渡邊勝 立命館慶祥高校 部活が終わって 素男と聡子がなにやら話している 素男 円筒の中に円錐 があるとするよ 底面が共通でさ 高さが同じ円錐の体積が円筒の体積三分の一というのがどうもおかしいよ
円錐の表面積 \begin{align*} S &= \pi r^2 \pi r l \\5pt &= \pi r^2 \pi r\sqrt{r^2h^2} \end{align*} 表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314 公式の導出方法と計算例については、「円錐の表面積の求め方」をご覧ください。 円錐の微小面積を教えて下さい。 球の微小面積はdSは、 R^2 sinθ dθ dR で表されます。 一方で、円錐の側表面の微小面積はどういう式で表されますか? 検索などして調べたのですが、分かりませんでした。 どなたか教えて下さい。 QVALUE お礼率12% (46/365直円錐の体積 直円錐の表面積 直円錐の側面積 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。 参考としてご覧ください。
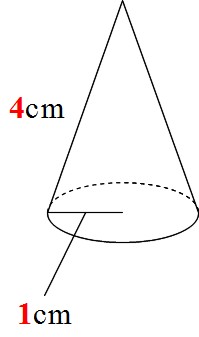



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐の表面積 側面積 体積の求め方教えてください Clear
円錐の側面積の求め方ですね。 円錐の側面積の求め方 母線×底面の半径×314 確かにこの公式を覚えておけば側面積を即答できるため、圧倒的に有利なのですが、それは覚えていられる間の話。 もし 忘れたり混乱したりすると、求められなくなって3)おうぎ形の面積を求める。 いろいろな円錐の側面積を求めよう。 中心角を求めなくても,円錐の側面積は求められそうだ よ。 建造物のモデルをつくる ために,建造物を円錐と みなして考えるという文 脈を設定する。 ペンキはムラなく塗って いること 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし




円錐の体積ってなんであの公式なの Webty Staff Blog




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐の中心角の求め方概要 扇部分の半径 (母線)・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める こんな感じだよ 既に知ってる「扇の中心角を求める問題」に変えてしまう っていうのがポイント! 扇の中心角の求め方を知らない人側面積=母線×半径×π =9×3×π =27π (㎠) 表面積=9π+27π =36π (㎠) 以上です! めちゃくちゃ簡単じゃないですか? 以上のように、、「円錐の表面積」の問題は 公式1つでとても簡単になります。 それでは今すぐ上の円錐の表面積を円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
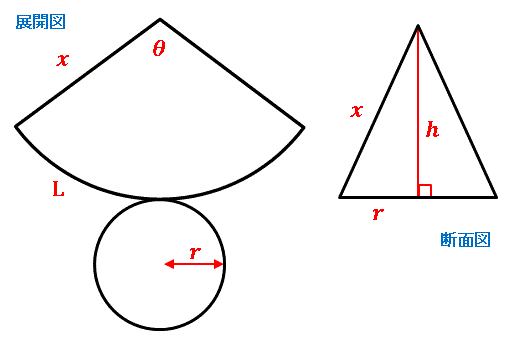



直円錐の体積




円錐の表面積 あんず学習塾のメモ 図表置き場
例題の円錐の側面積をこの公式で計算すると、 15π㎝² あっという間に円錐の側面積が出せました! これに底面積をプラスすれば、円錐全体の表面積も簡単に出せるのです。 円錐全体の表面積を、もっともっと簡単に計算する公式 先ほどのA = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐




円錐の表面積 Youtube




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月




毎日問題を解こう 27 苦手な数学を簡単に




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
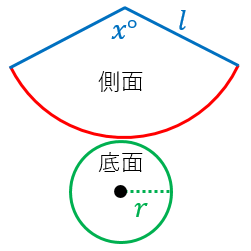



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
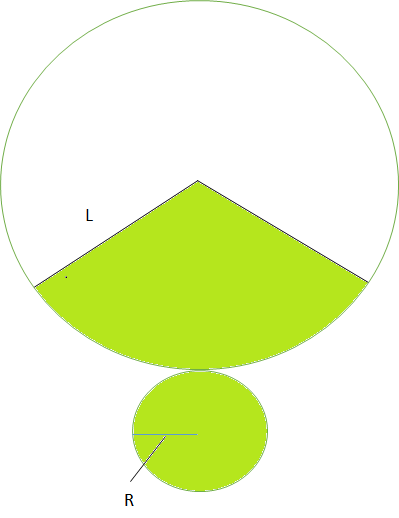



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




立体の体積 無料で使える中学学習プリント




公式を図解 すい体の体積 円すいの表面積の求め方




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積の求め方 公式と計算例



1




円錐台 Wikipedia




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




角錐 円錐の体積と表面積の公式 数学fun




円錐台の体積 側面積 香料ゐっすゐの夢
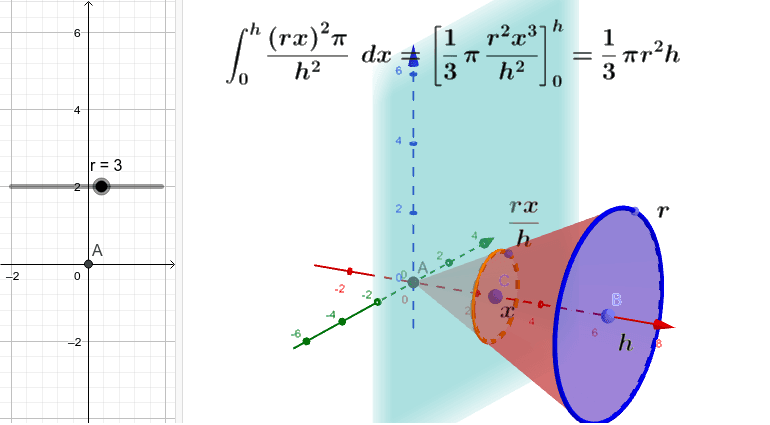



円錐の体積の求め方 Geogebra
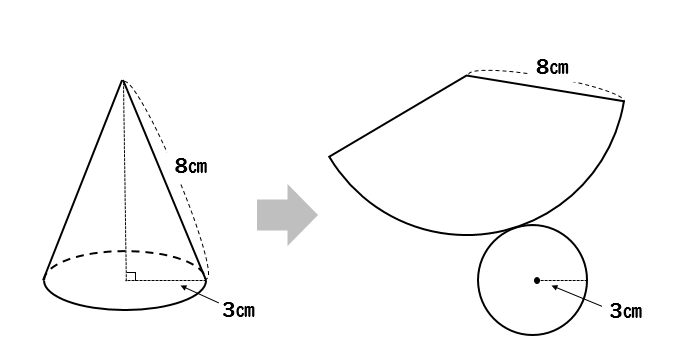



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方



円すい台側面積の公式を導く



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun
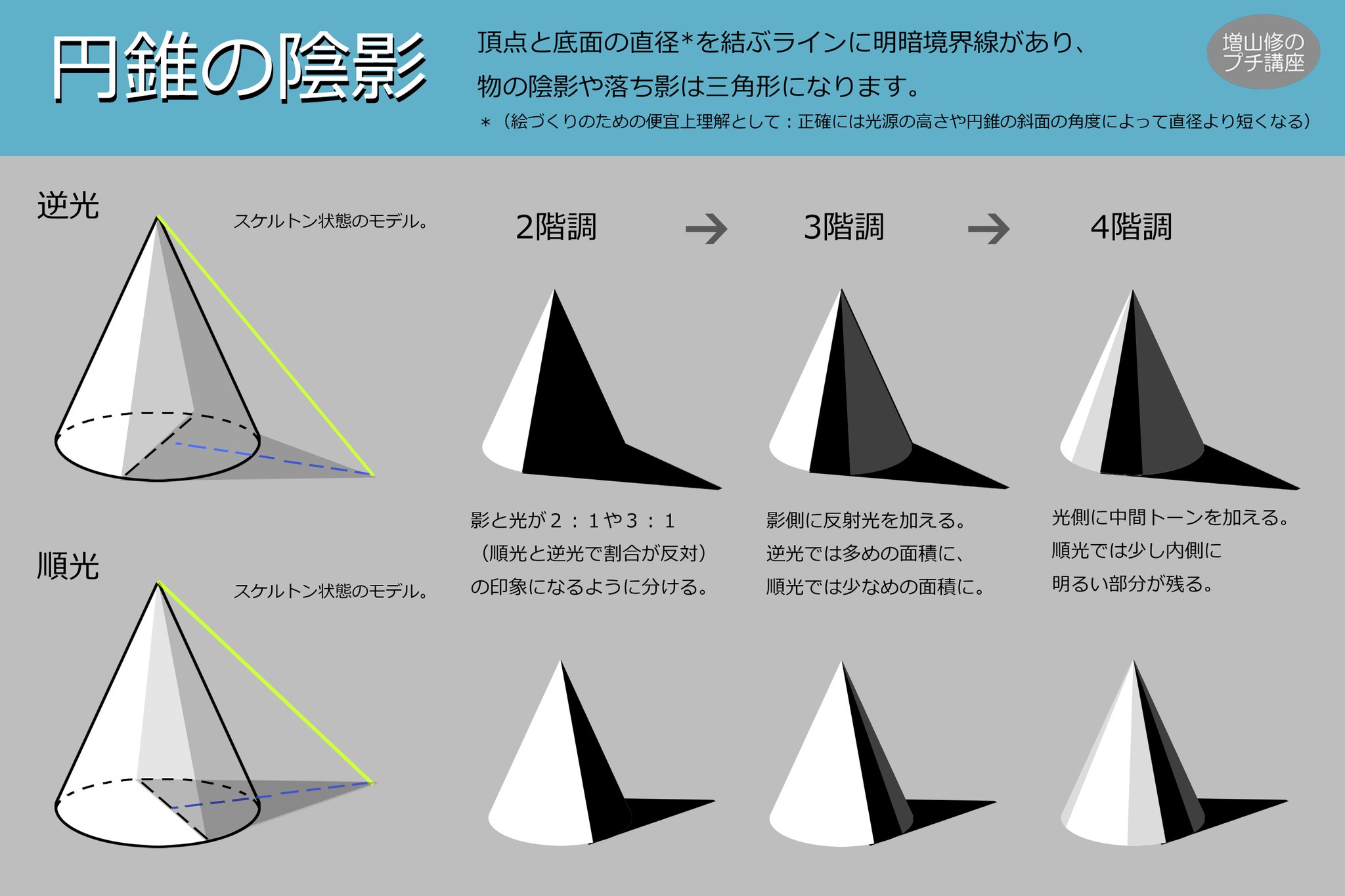



増山修 インスパイアード Masuyama Osamu Inspired Inc 円錐の陰影の付け方 側面が円柱と違い斜めなので 太陽光が当たりやすくなります そのため正確には底円直径より陰寄りに明暗境界線が出来ます しかし絵的な印象では光と影の面積比のほうが




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
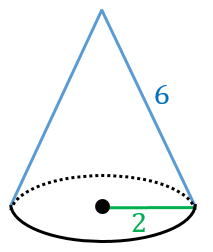



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 You Look Too Cool
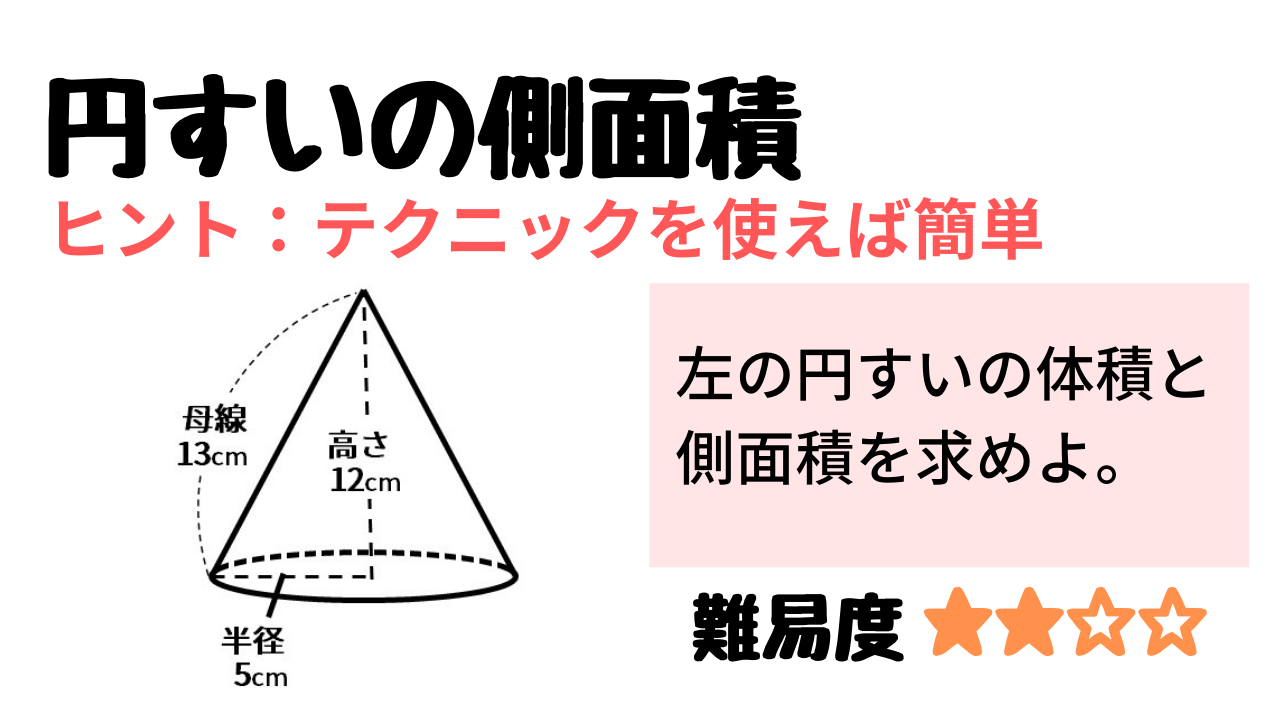



中学受験算数 円すいの側面積の問題 テクニック伝授 Stupedia




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
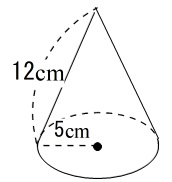



円錐 すい の表面積や四角錐 五角錐の体積の求め方




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear
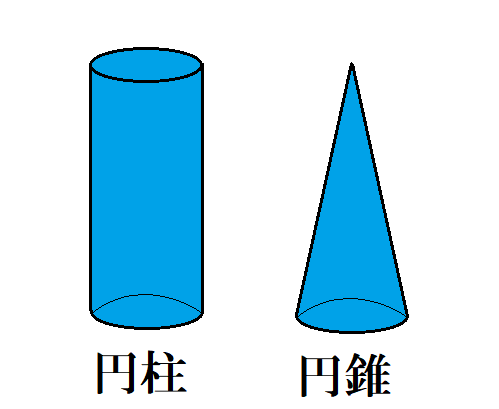



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋all Rights Reserved




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積の求め方 公式と計算例




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円錐の側面積 中学から数学だいすき




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su
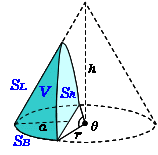



一部が欠けた直円錐の体積 高精度計算サイト



1




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo



5 10 おうぎ形の展開図から母線 半径 中心角を求めるには さんすうがく
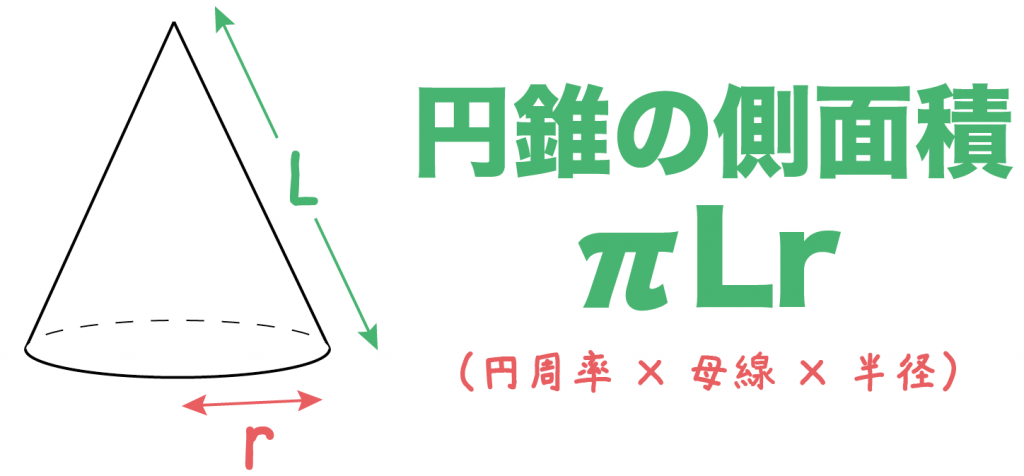



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



1



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順
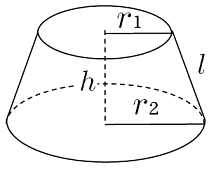



初等幾何 円錐台の側面積を求める 大人が学び直す数学
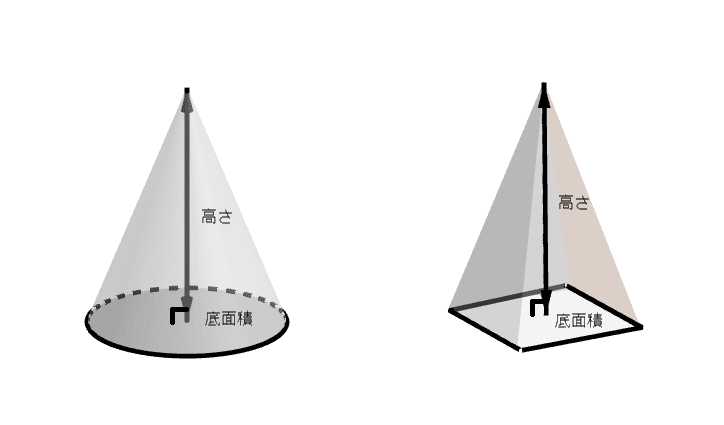



錐体 錐体 円錐 角錐 の体積 底面積 高さ 3 ワンセンテンス算数 Note




公式を図解 すい体の体積 円すいの表面積の求め方




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




この問題の円錐の底面積の半径の求め方を教えてください Clear




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円すいの展開図 側面積の求め方 公式を使って15秒で解こう



球の表面積 アルキメデスの方法 4の2 セルフ塾のブログ




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



図形 円錐の側面積の求め方 名古屋市北区の学習塾は思考力を育む 泰成スクール
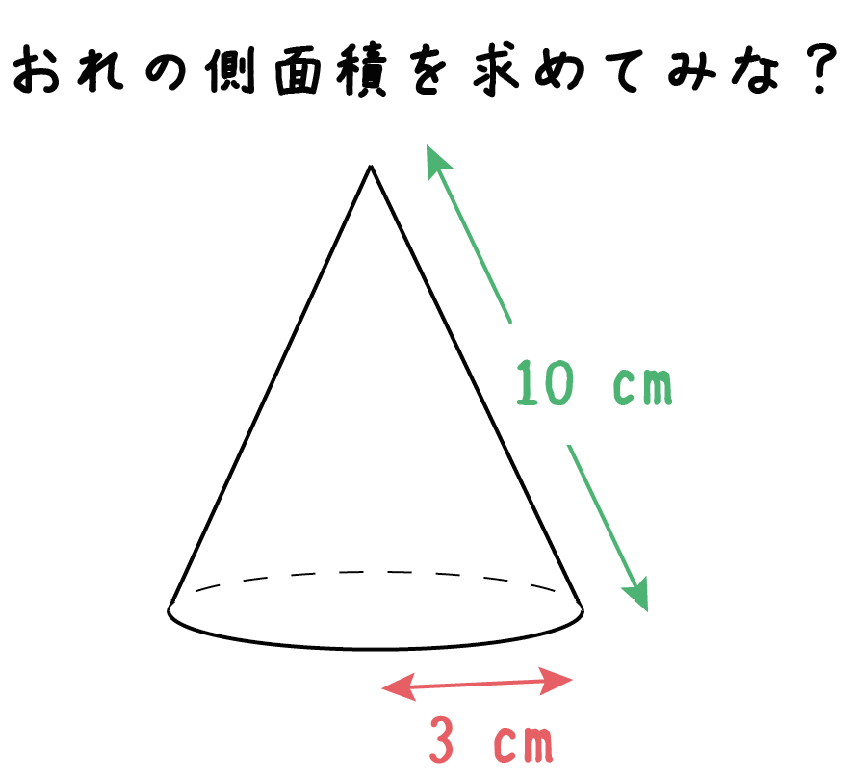



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 円すいに関する練習問題



円錐の側面積の求め方 インターネット家庭教師のアスミラ




中3 三角形の相似 円錐の体積比 日本語版 Youtube




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー




直円錐の体積 高精度計算サイト




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋



円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円錐とは 体積 表面積の公式や求め方 受験辞典
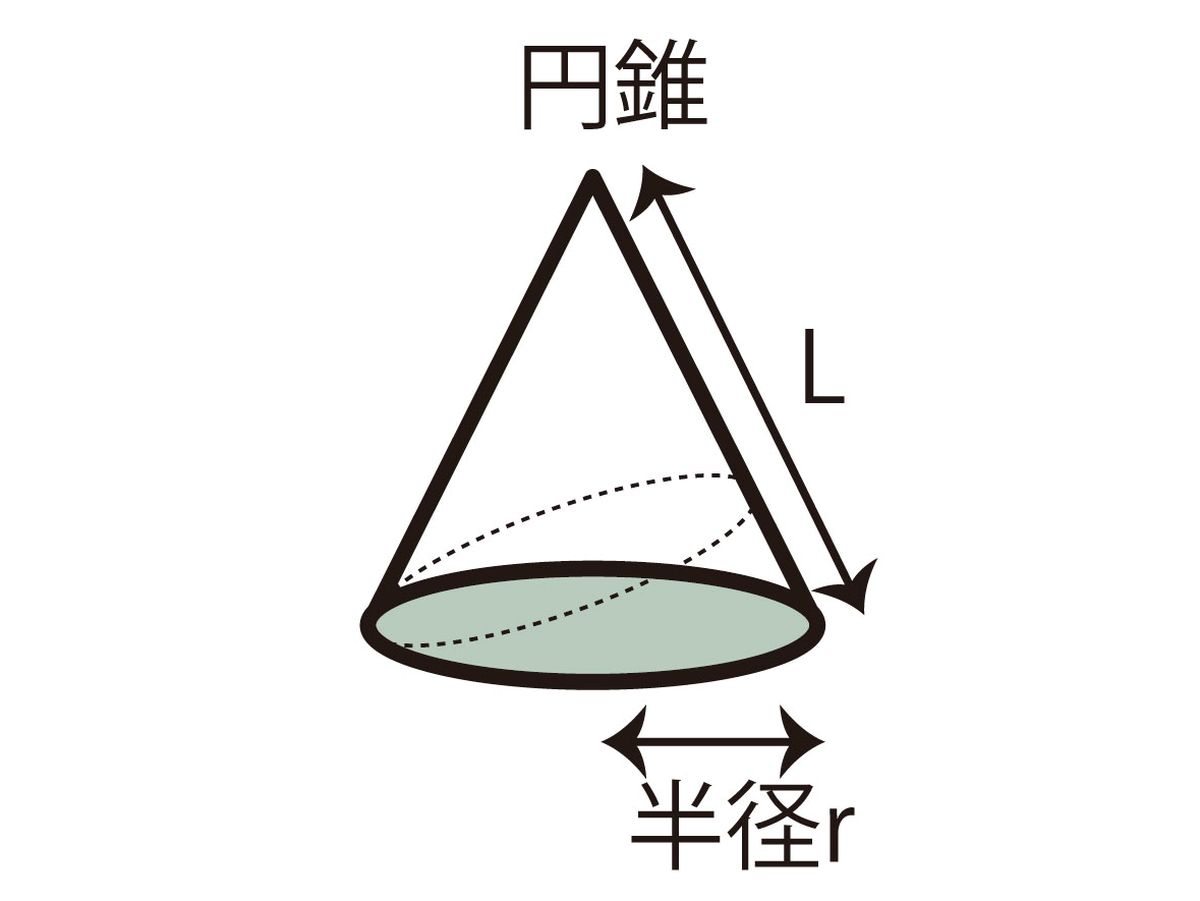



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋




円錐の表面積を 公式を使って求める チーム エン
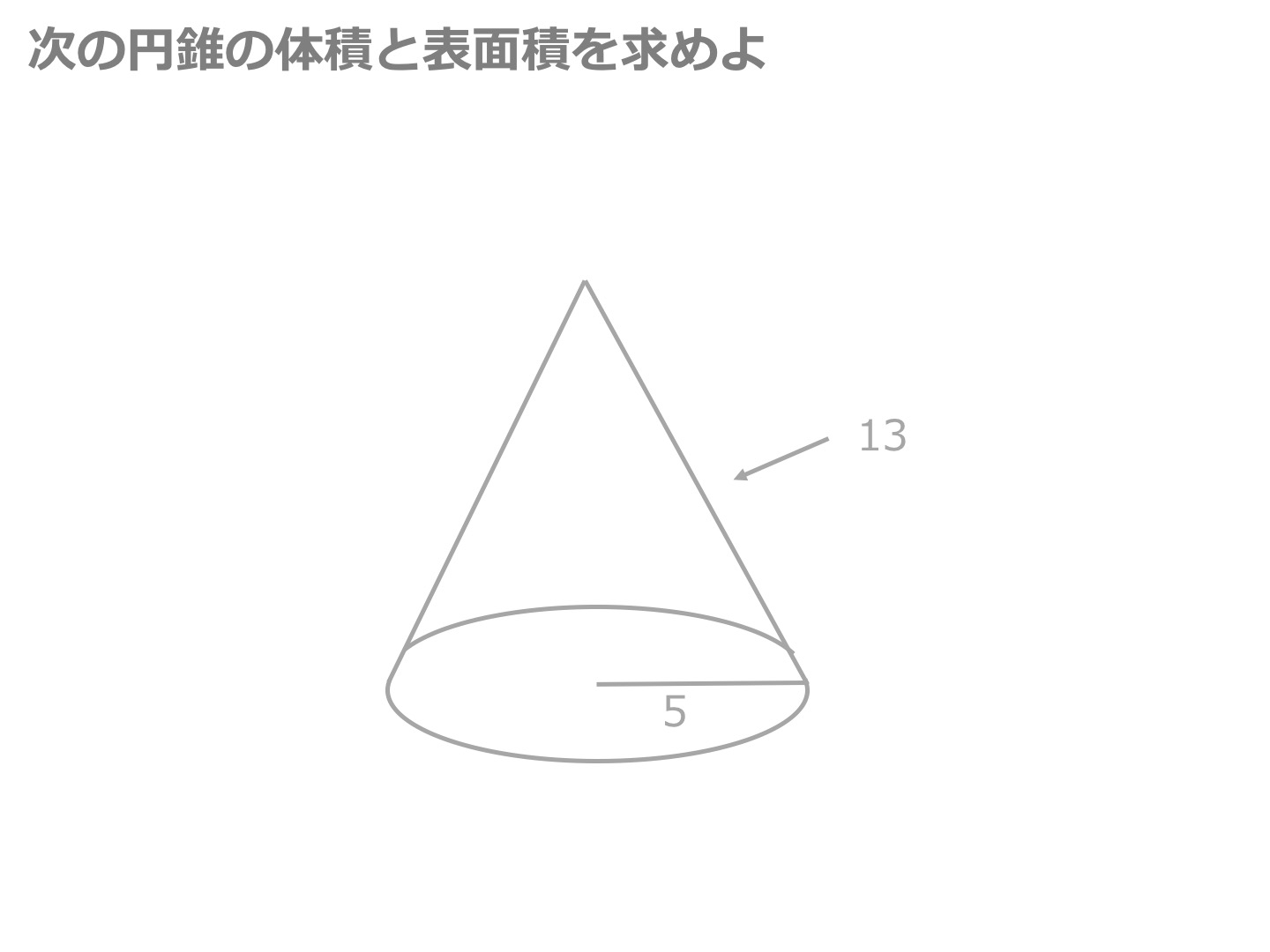



3分でわかる 円錐の体積 表面積の求め方 合格サプリ




中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中1数学 Youtube



0 件のコメント:
コメントを投稿