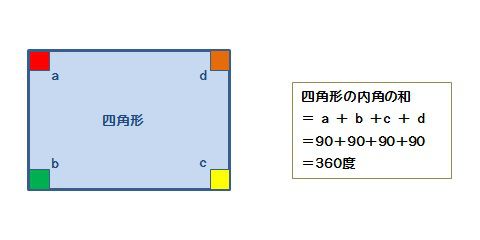
本時の目標:三角形の内角の和をもとに、四角形の内角の和を求める 単元「合同な図形」(5年) 前は三角形、今回は四角形。三角形の時も、中にある角を求めたよ。 教師:(本時の学習で)これまでと違うところ、似ているものを探しまし ょう。三角形の内角の和が 180°であることを見出す考 えで,演繹的な考えとは,三角形の内角の和を基 に,四角形の内角の和を求める考えである。 児童について 「きまりを見つけて」の学習から,「帰納的に考え る」ことができた児童は757%であった。児童の三角形の内角の和は 180 ∘ でしたが、 四角形の内角の和は必ず 360 ∘ になります。 例えば、長方形や正方形は、全ての角度が 90 ∘ であり、全て足すと 90 90 90 90 = 360 ∘
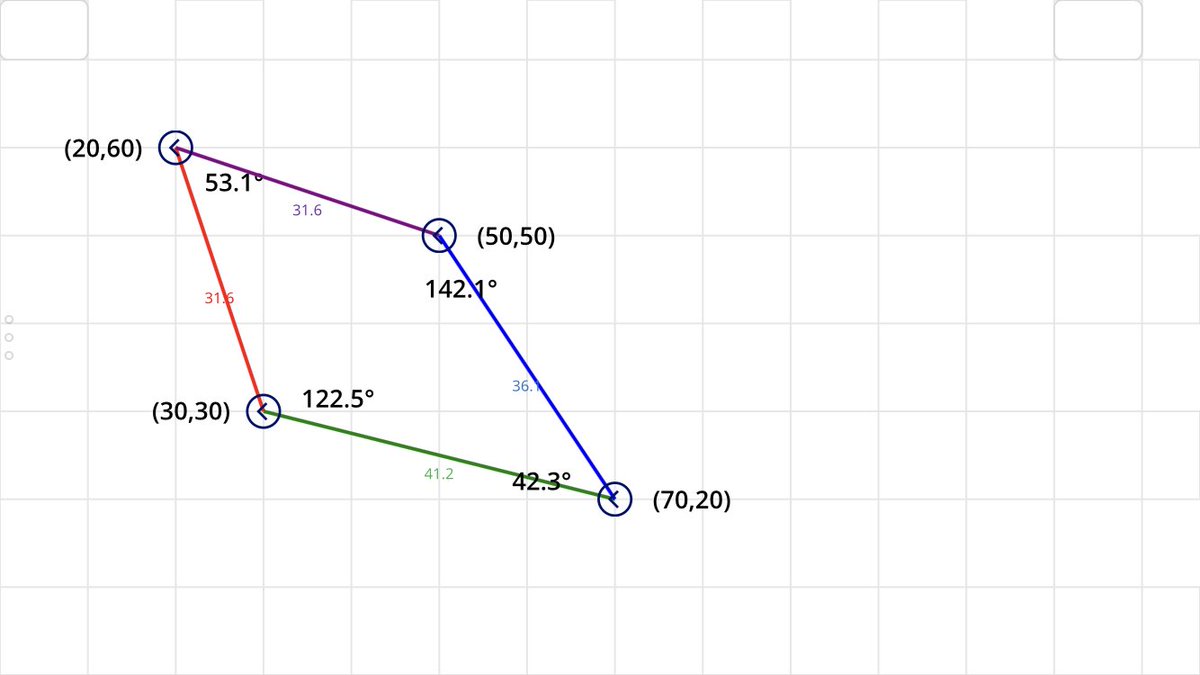
Hiro 四角形の内角の和は常に360です とか 平行四辺形は向かい合う角の角度が一緒で隣り合う角の和は180です みたいな教育に最適じゃないか いいもの作った 自画自賛
四角形 内角の和 証明
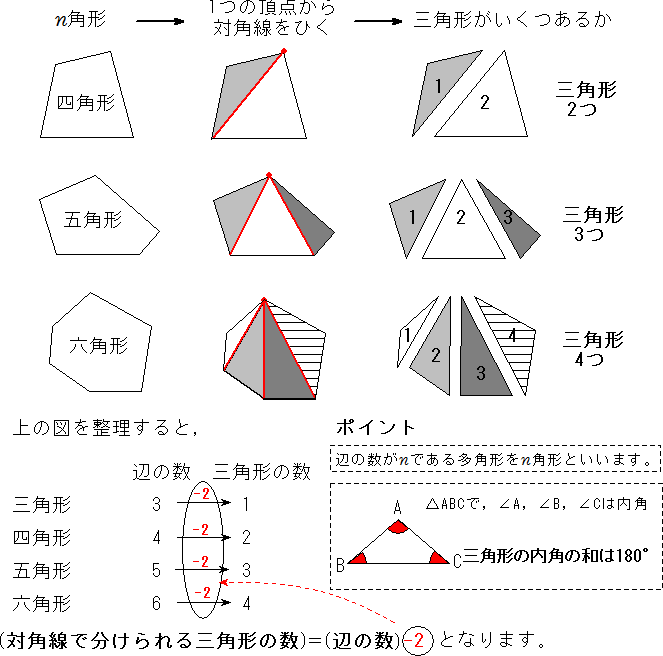
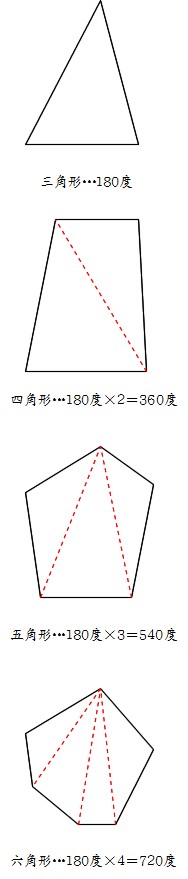
四角形 内角の和 証明-三角形の内角の和180°を使って多角形の内角の和を考えます。 一つの頂点から他の頂点に補助線を引いて三角形に分けます。 四角形 →三角形2つに分けられる →三角形3つに分けられる 五角形 →三角形4つに分けられる 六角形 四角形の内角の和はは三角形生「四角形の内角の和」の授業実践事例から他者の図を理解し,視覚的に伝え合う こと(ビジュアルコミュニケーション)で児童が読みとる力を伸ばす児童の姿があ るか質的研究を目的としたものである。その結果, r四角形の内角の和を三角形の
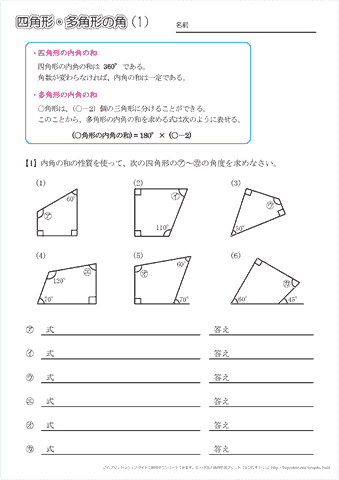



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
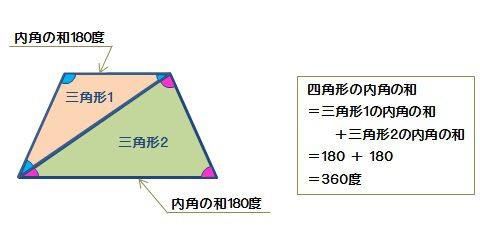
①三角形の内角の和が180°になる ①三角形の内角の和が,180°であ ①三角形や四角形の内角の和に ことや,四角形の内角の和が360° ることを帰納的に見出している。 ついて,筋道立てて考えよう になることを理解している。①三角形の内角の和を基にして,多角形の内角の和を求める方法を考える力 ②図や式,言葉を使い,根拠を明らかにしながら,考え方や求め方を筋道立てて説明する力 三角形・四角形の内角の和においては,敷き詰めや切って合わせる具体的な操作を通して,「いろいろな三角形(四角形) の内角の和が180°(360°)になる」ことに気付かせ,「どんな三角形(四角形) でも内角の和は180°(360°) になる」ことに導く。しかし,五角形以上の多角形では, 操作活動よりも計算で求める方法が有効になる。そこで,四角形の内角の和の求め方を考え, 説明する学習に重点を置き, 多角形の内角の和を求めるための考え方の素地を作る。 四角形の内角の和については,三角形の内角の和を利用し,「三角形の内角の和は180°。四角形を2つの三角形に分けると,四角形の内角の和は三角形の内角図形の性質─四角形の内角の和(5年生) ねらい ・三角形の内角の和(180°)を基にして、四角形の和が360°になることを演繹的に説明させる。 ・条件を変えながら、新しいものの見方にかかわろうとする態度を育てる。
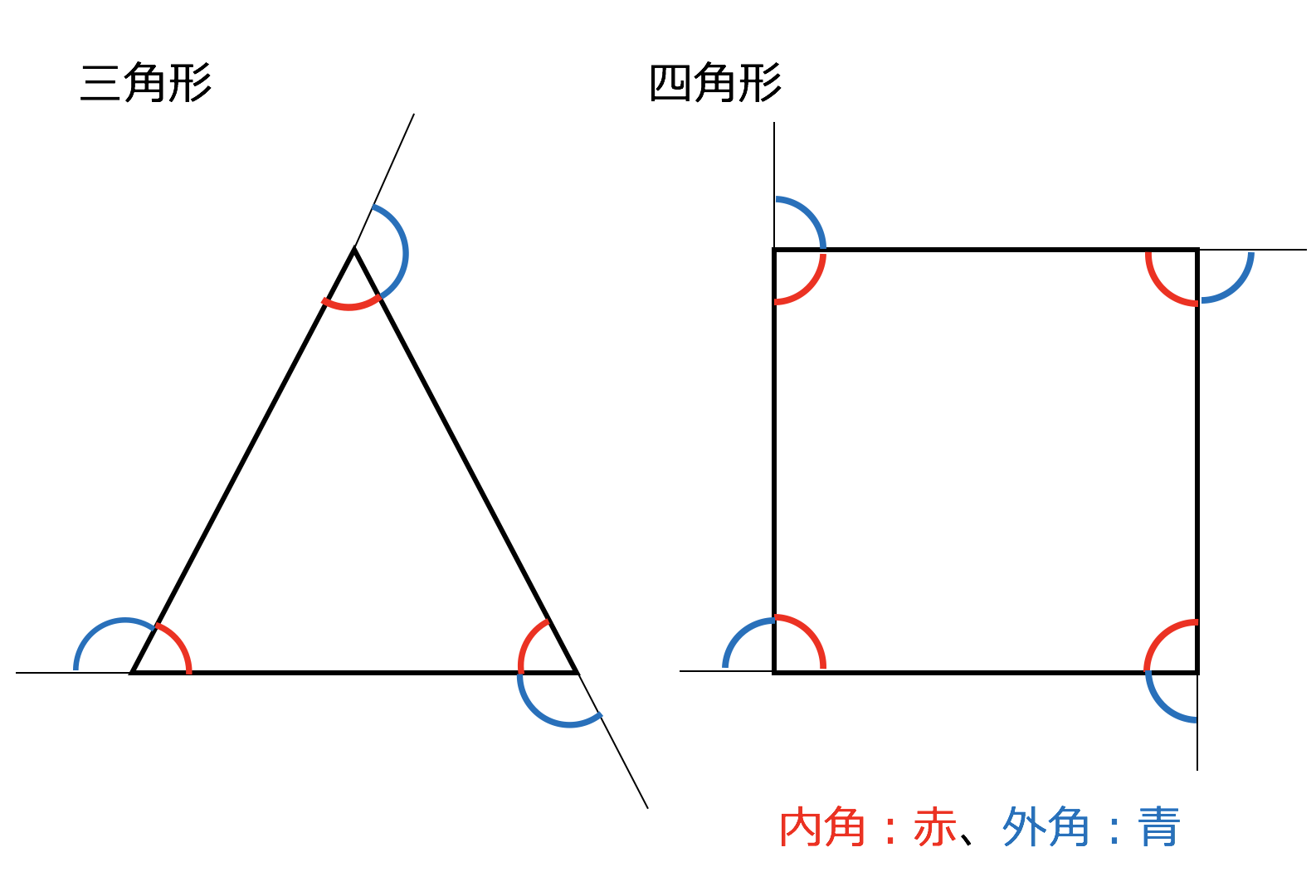
四角形の内角の和は? 四角形の内角の和は360°です。四角形には、 ・長方形 ・正方形 ・ひし形 ・平行四辺形 など色々な種類がありますが、全て内角の和は360°です。 多角形の内角の和は?1分でわかる公式、問題の求め方、簡単な証明 まとめ①四角形の内角の和を三角形の内角の 和の求め方や三角形の性質を用いて 求める。 ②四角形の内角の和の求め方を活用 し、五角形の内角の和を求める。 ③3つの角の大きさがわかっている四 角形の、もう1つの角の大きさを分 度器を使わずに求める。四角形ではそれが4組あるので、図の赤と青すべての角の和は180×4=7 青の角は内角なので四角形の内角の和360 赤と青の和7から青の和360を引くと7360=360 よって四角形の外角の和は360°となります。 同様のことを五角形でやってみると
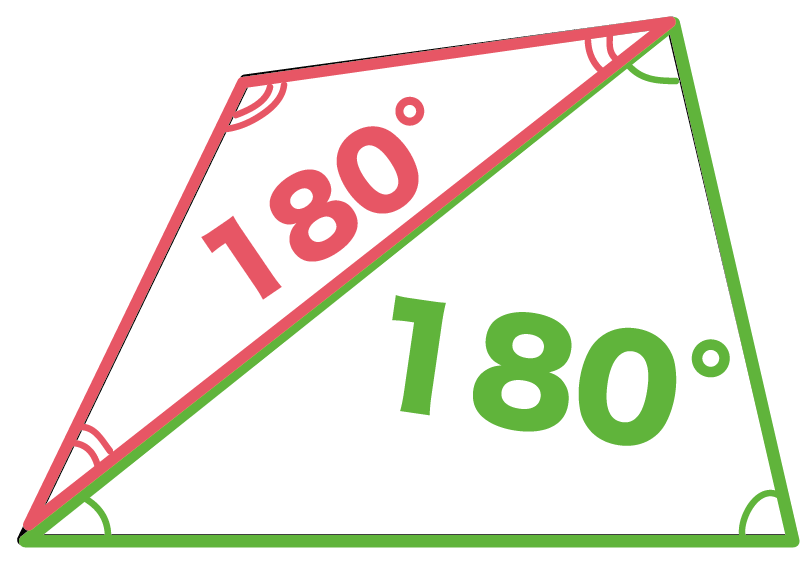
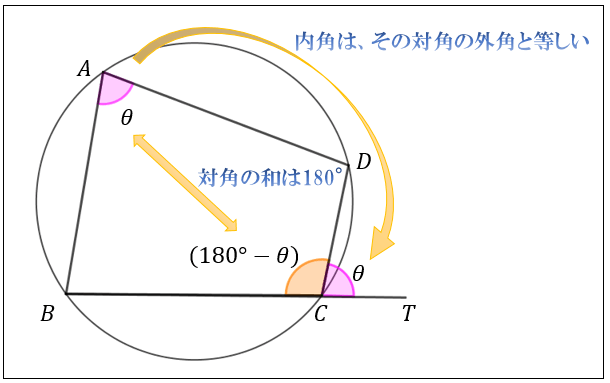
● 円に内接する四角形の内角は、その対角の外角と等しい まず、円に内接する四角形では ∠ A ∠ C = 180 ° が成り立ちます。 対角の和が 180 ° になる理由は、 円周角の定理 から説明できます。 円の中心を点 O 、 ∠ A = θ とおくと三角形の内角の和は180°だったよね? このことを利用して四角形の内角の和を調べよう。 一つの頂点から対角線を引いて、二つの三角形に 分けてみよう。四角形の内角の和が360°であることを基にして、いろいろな四角形の角度(内角・外角)を計算で求める。 ・大きさの分かっている角に着色させ、求めたい角をとらえさせるとともに、判明した角度を記入させる。 2ページ参照 ⑤三角形の内角の和が180°で
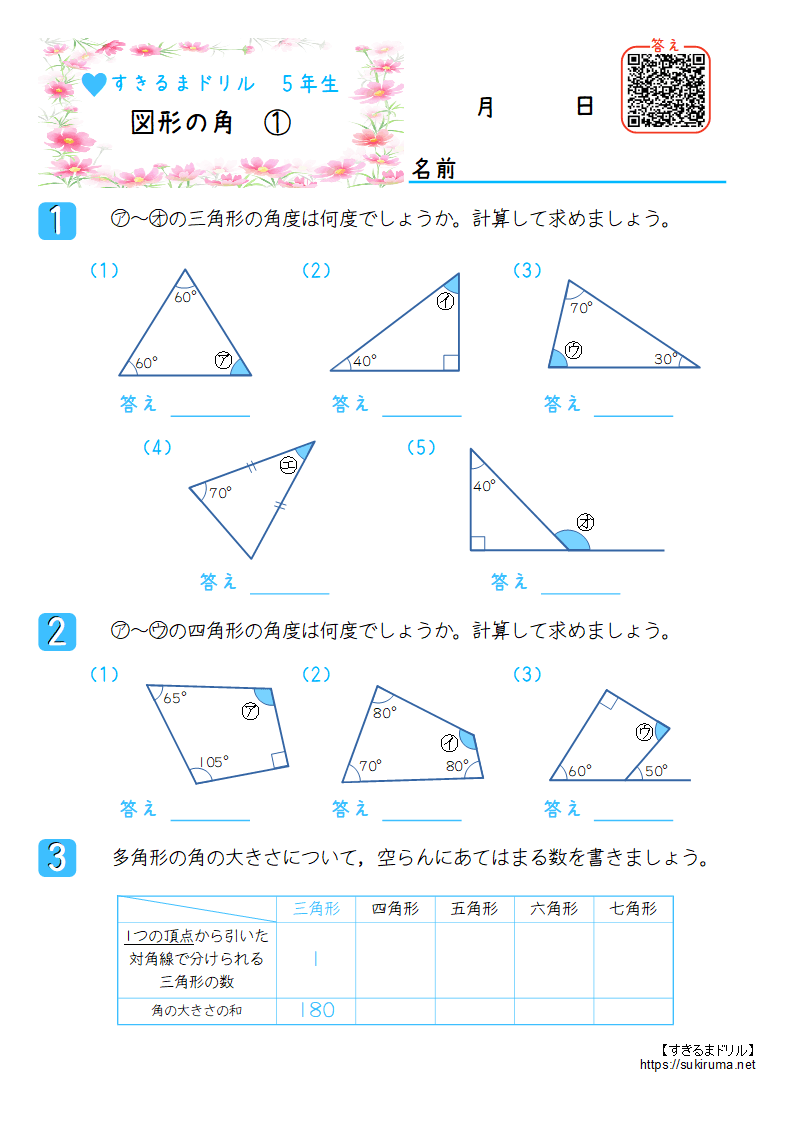



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント
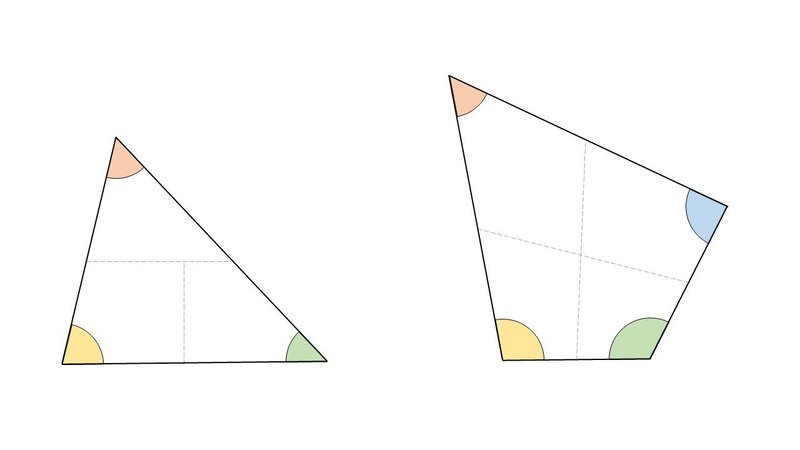



算数工作 三角形と四角形の内角の和を調べてみよう 外角の和のデータも公開中 Math Channel Note
三角形・四角形の内角と外角 三角形、四角形の外角を知り、外角の和が360°を確認する ABCの外側にあるので ∠Cの外角 といいます。11角形 16° 12角形 1800° 5角形までの内角の和は覚えましょう。 多角形の内角の和は下の公式で求められます。 角形の内角の和 = 180 × ( 2) 例えば8角形の内角の和は 180 × (8 2) = 1080三角形の内角の和のきまり(180°)を考える。 第2時 いろいろな三角形の角度の問題を解く。 第3時 切って貼る・折る・分度器で実測する方法で四角形の内角の和を求める。 第4時 四角形の内角の和を正確に求める方法を考える。 第5時
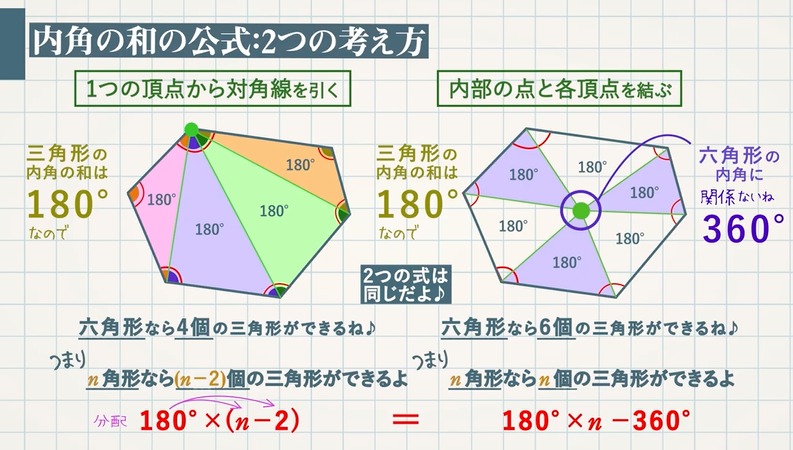



内角の和 180 N 2 外角の和 360 教遊者




四角形の内角の和 授業のポイント 算数を究める
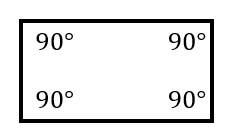
四角形の内角の和を考えるときは 長方形や正方形で考えるのが簡単だと思います。 長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 » この記事の続きを読むの和を三角形 の内角の和を もとに説明し ている。(ア、 ウ、エ) 五角形や六角 形の内角の和 は、三角形の内 角の和をもと にして求めら れることが分 かる。(ア、イ、 ウ) 5 単元の学習内容についての理解 を確かなものとする。 ・ 三角形、四角形の内角の 多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されま



中学数学円の中の四角形の向かい合う内角の和は 180度と習ったので Yahoo 知恵袋
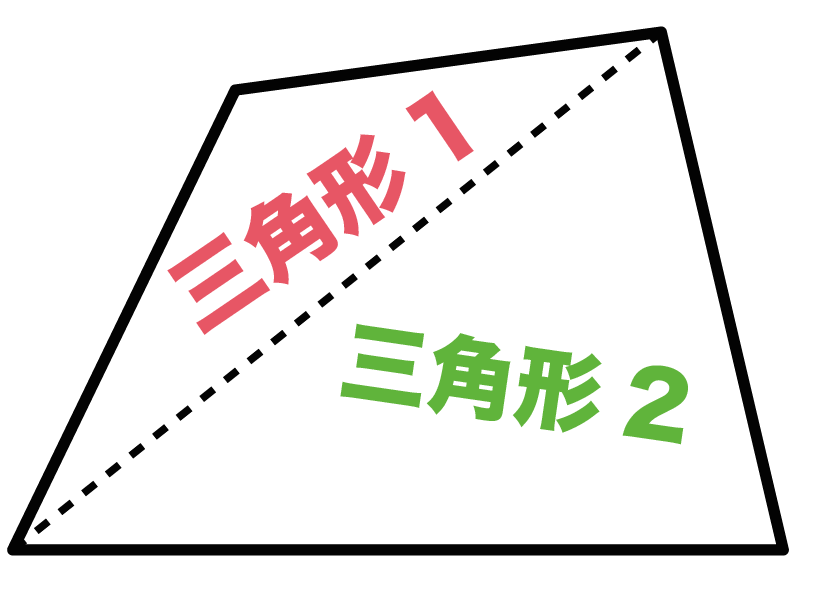



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく
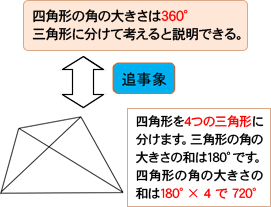
三角形の内角の和が180度なのは知っていますよね? その三角形が2個あります。 つまり、 三角形1と三角形2の内角の和の合計が 四角形の内角の和 になるということ。したがって 四角形の内角の和=360度 となるのです。特徴 一般的には矢型、楔型などで呼ばれる。 四角形abcdにおいて、∠a,c,dの合計が角bの外角に等しくなる。 また、点bを中心とする円が点a,c,dに内接する場合、∠bの外角は∠dの2倍である。 証明 点d,点bを結び、∠bdcを∠f,∠cbdを∠l,∠bdaを∠h,∠abdを∠s,∠bの外角を∠xとすると、さて,三角形の内角と外角について,次の重要な事実が成り立ちます. 三角形の内角と外角の性質: (1) 三角形の内角の和は $180°$ である. (2) 三角形の外角は,それと隣りあわない $2$ つの内角の和に等しい. これを証明してみましょう.



三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト
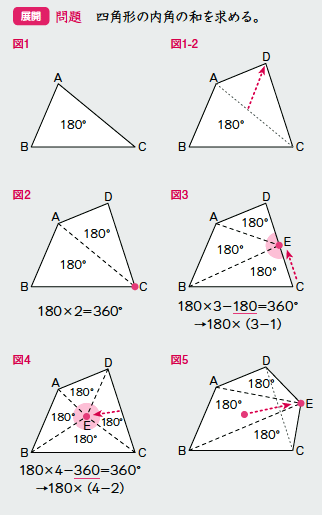



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所
四角形の内角の和のいくつかの求め方は教科書にも紹介されているが、個々の求め方が独立して扱われがちである。 PC を利用して、図形を動的 に見せることによって、それらの考え方に児童自らが気付いたり、考え方同士の関係を見い出したりすることが他の多角形の内角の和を説明することができる。 (3) 単元の評価規準 知識・技能 思考・判断・表現 主体的に学習に取り組む態度 ・三角形の3つの角の大きさ の和が180度になること や,四角形の4つの角の大 きさの和が360度になるこ とを理解している 四角形は対角線をひくと、2つの三角形に分けることが出来ます。 三角形の内角の和は180°なので、四角形の内角の和は 180×2=360° となります。 平行四辺形の場合 平行四辺形は向かいあう角の大きさが等しいので ア+イ=180° となります。 外角がわかっ
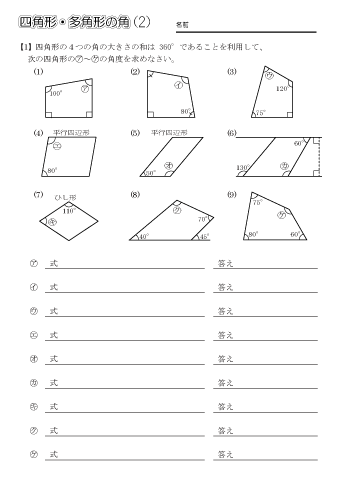



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
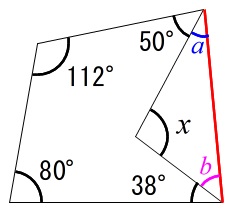



多角形の内角の和の公式と外角の和を利用した角度の求め方
・三角形の内角の和が180°であることや、四角形の内角の和は三角形に分けることによって求められるこ とを理解する。 (知識・理解) 3.指導にあたって (1)児童について 1学期には「形も大きさもじ図形を調べよう」で、合について理解 し、作図を



ドリルズ 小学5年生 算数 の無料学習プリント四角形の角



Www Pref Kochi Lg Jp Soshiki Files File 1 Pdf




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




多角形の内角の和 外角の和の公式 数学fun
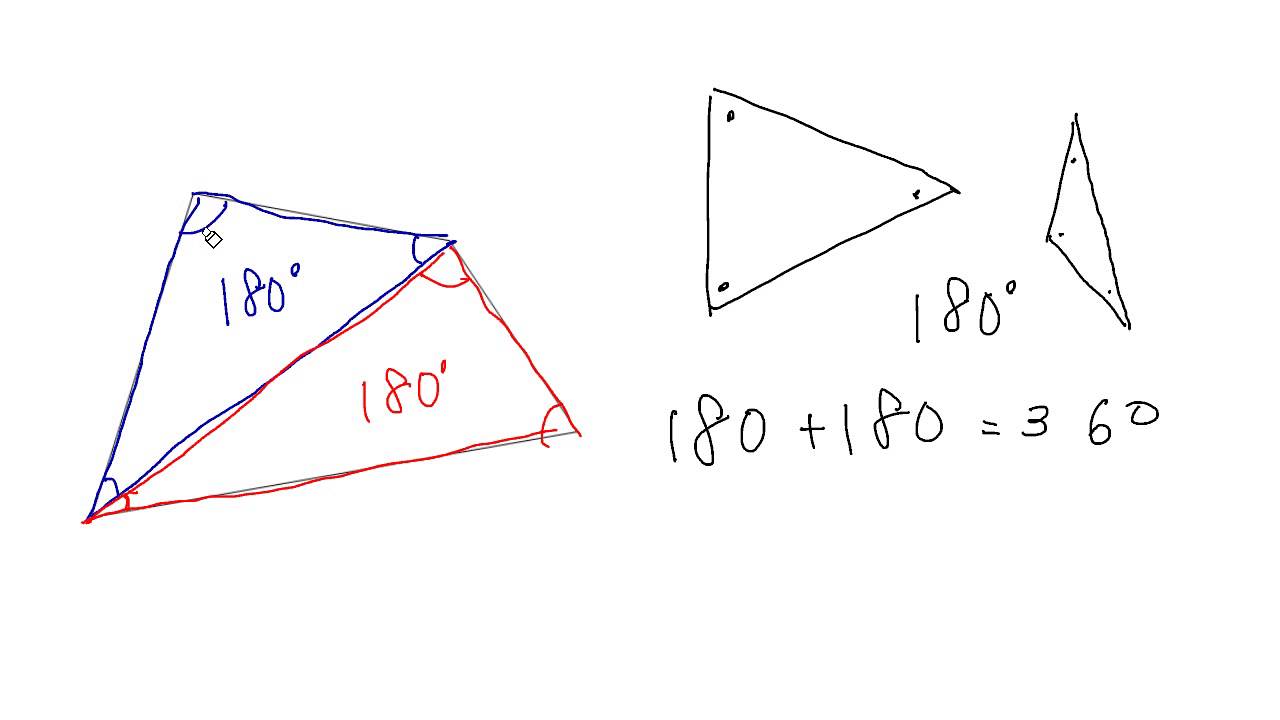



四角形の内角の和 Youtube
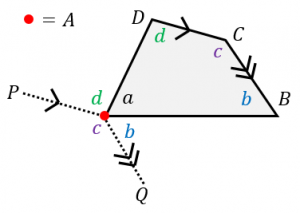



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学



5年 四角形のふしぎ 算数イメージ動画集 大日本図書




小学校5年 算数 四角形の内角の和 Youtube




四角形の内角の和 授業のポイント 算数を究める
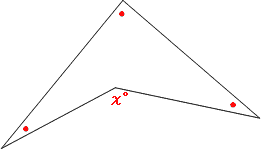



角度の求め方 算数の教え上手 学びの場 Com
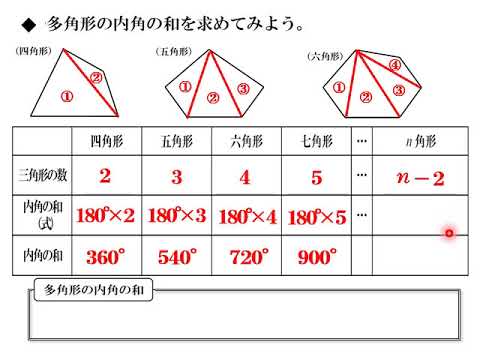



動画 多角形の内角の和 Youtube




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
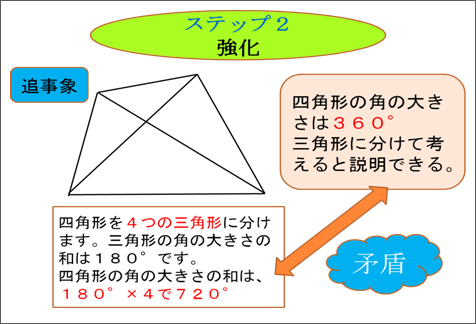



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




Hiro 四角形の内角の和は常に360です とか 平行四辺形は向かい合う角の角度が一緒で隣り合う角の和は180です みたいな教育に最適じゃないか いいもの作った 自画自賛




内角の和 180 N 2 外角の和 360 教遊者




四角形の内角の和 授業のポイント 算数を究める




四角形の内角の和 授業のポイント 算数を究める



円に内接する四角形



1




内角の和 180 N 2 外角の和 360 教遊者
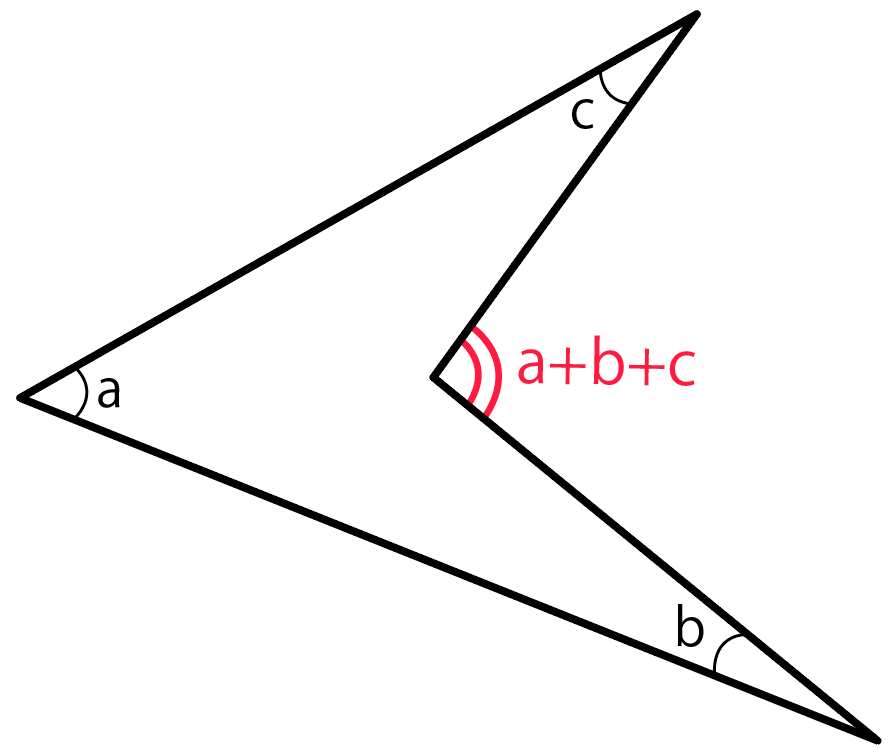



ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
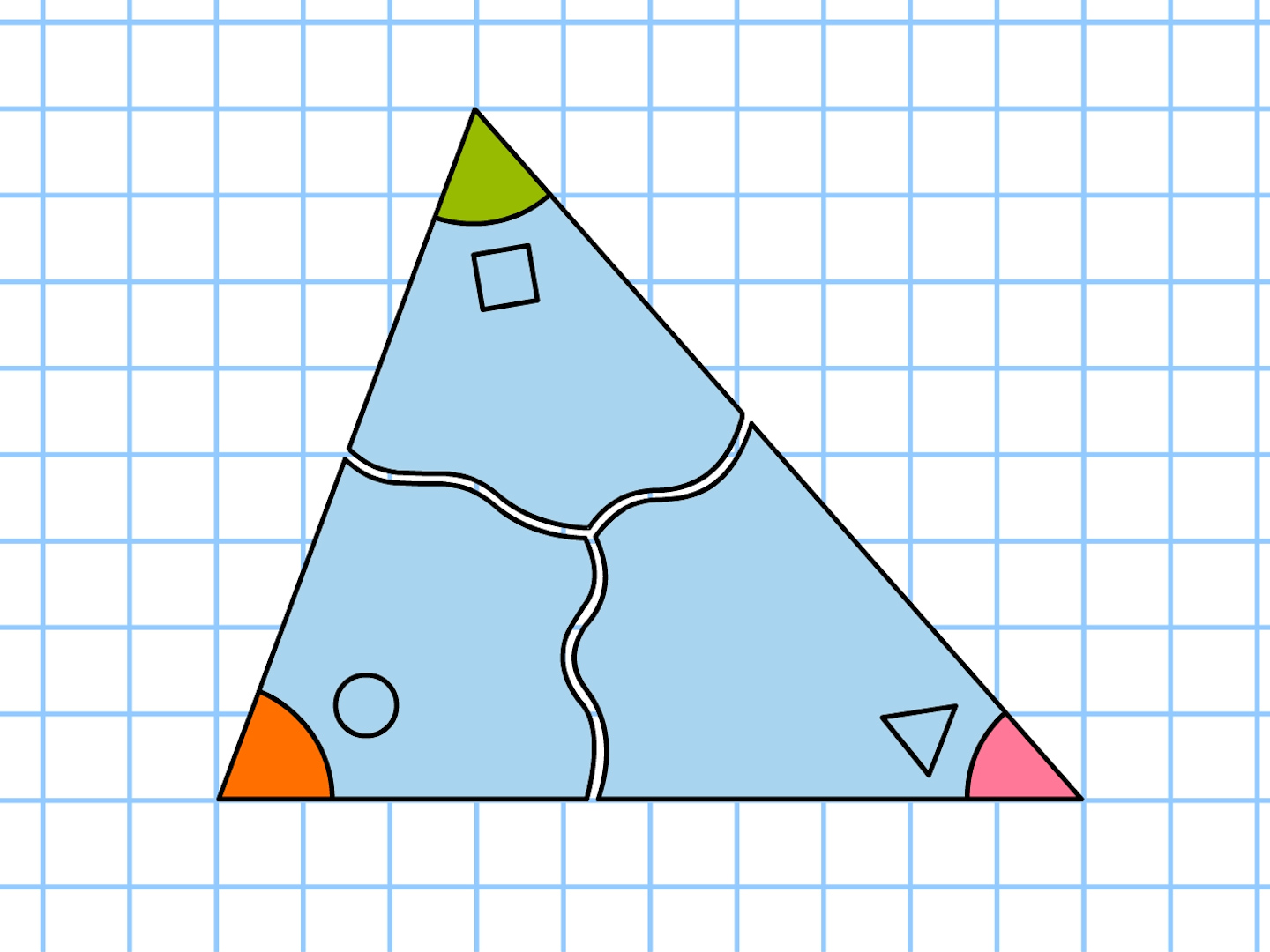



5年 三角形のふしぎ 算数イメージ動画集 大日本図書




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく
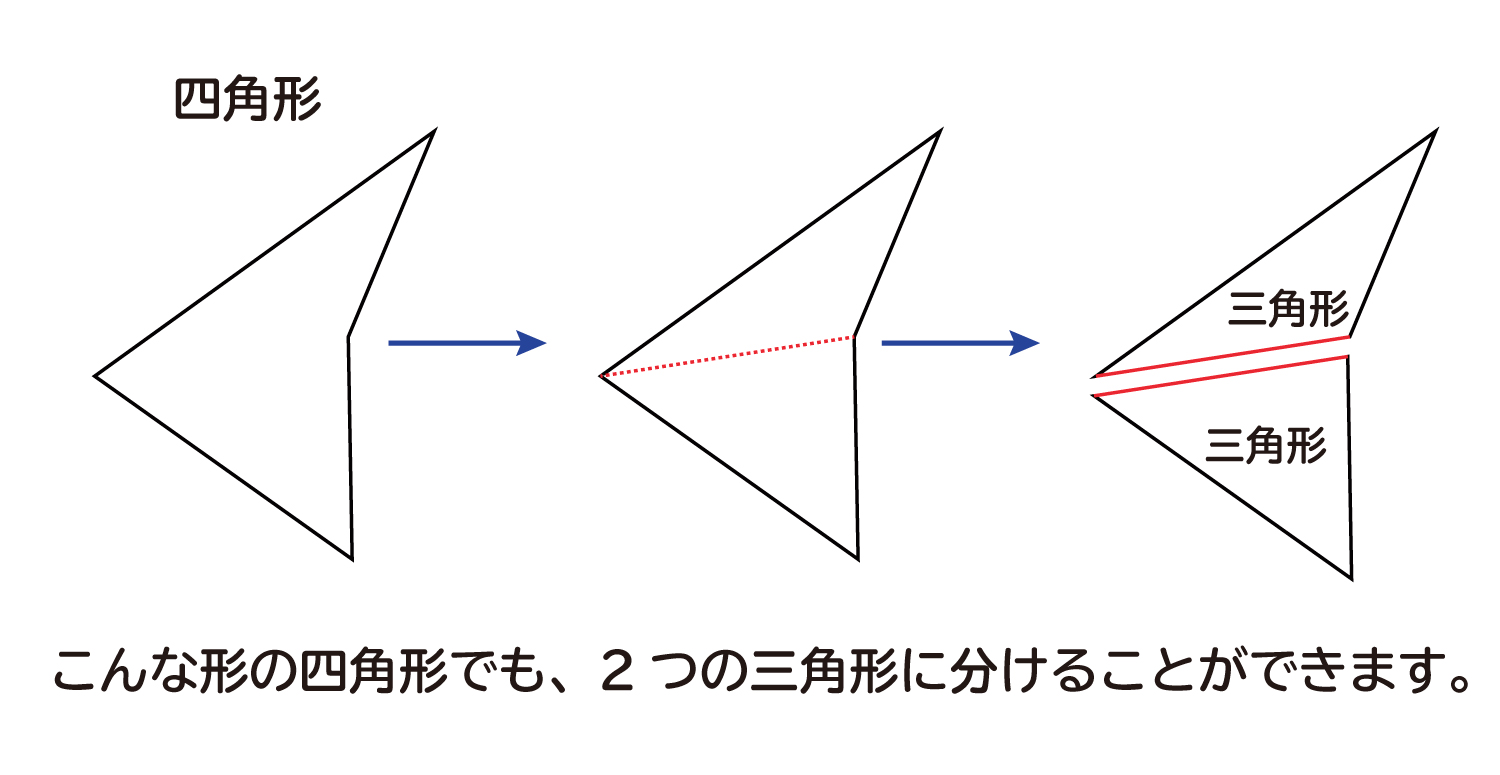



多角形の内角の和 は何度なのか を説明します おかわりドリル




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




四角形の内角の和を求める問題で 四角形に 三角形を上に足して求める方法が理解 Clear




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




多角形の内角の和 は何度なのか を説明します おかわりドリル
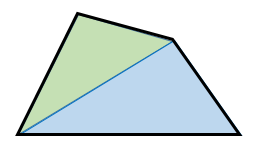



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学



Http Www Kochinet Ed Jp Shimizu E Kounaikensyuu H28zissenzirei5nen Pdf



多角形の内角の和 勉強ナビゲーター




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア
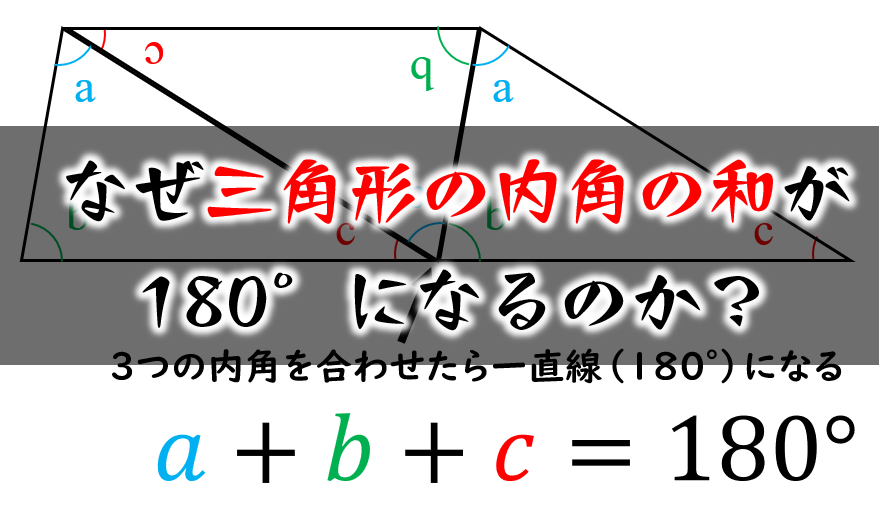



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
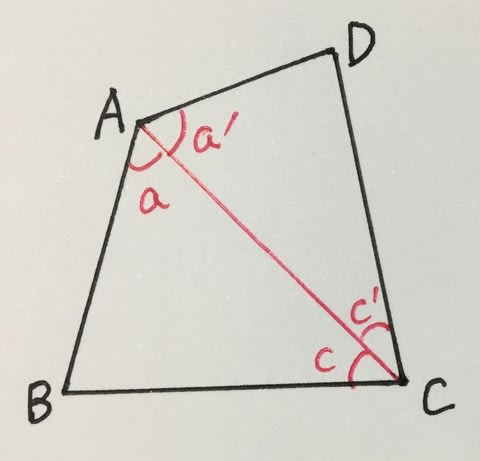



多角形の内角の和 四角形 Takapの数学日記



Http Www Kochinet Ed Jp Shimizu E Kounaikensyuu H28tangenkoso5nen Pdf




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題




多角形の内角の和 外角の和の公式 数学fun




中2 中2 数学 内角の和 授業ノート 中学生 数学のノート Clear
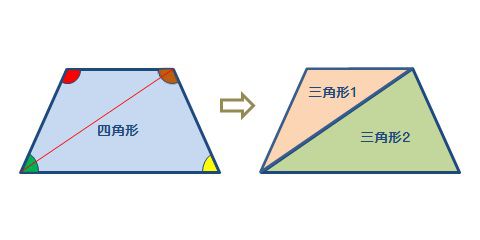



四角形の内角の和 算数の公式覚えてますか
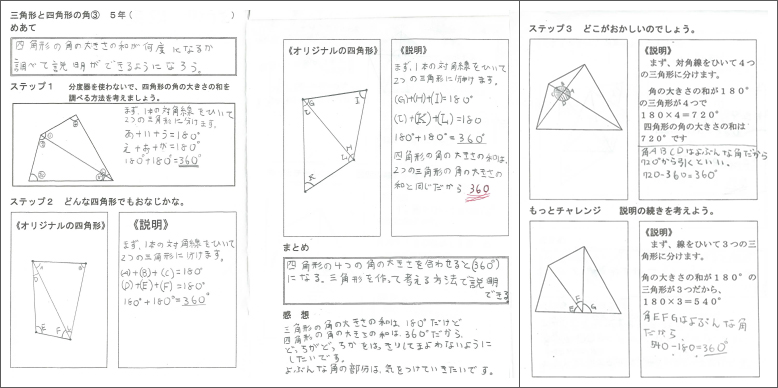



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




四角形の内角の和 スクールプレゼンター教材共有サイト スクプレ道場



四角形の内角の和 算数の公式覚えてますか



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




内角の和 算数用語集




多角形の内角の和 算数の公式覚えてますか




中学2年生の数学 内角の和 外角の和の復習 塾講師が数学をやりmath



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



Math 多角形の内角の和 働きアリ




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




算数工作 三角形と四角形の内角の和は何度 実際に切って確かめてみよう パラパラ漫画風動画 Youtube




朝日新聞デジタル 内角の和 わくわく360度 花まる先生公開授業 教育




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角



四角形の内角の和 算数の公式覚えてますか




多角形の内角の和 算数の公式覚えてますか




小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生



Math 多角形の内角の和 働きアリ The 2nd




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



1



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




内角の和 180 N 2 外角の和 360 教遊者




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版



1



ブーメランのような形をしている四角形 三角形 の内角の和は普通の四角形の内 Yahoo 知恵袋



1




n角形の内角の和 中2 多角形の内角と外角 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学




多角形の内角の和 は何度なのか を説明します おかわりドリル



Http Www Sendai C Ed Jp 02kensyu 02cyoken H27 Yoshida S Pdf




四角形の内角の和 授業のポイント 算数を究める
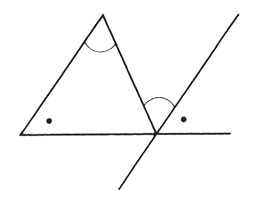



内角の和 算数用語集




多角形の内角の和の公式と外角の和を利用した角度の求め方




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく
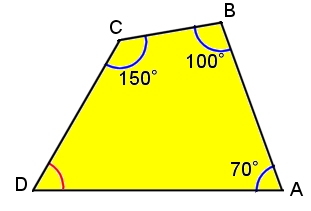



いろいろな問題




四角形の内角の和 授業のポイント 算数を究める
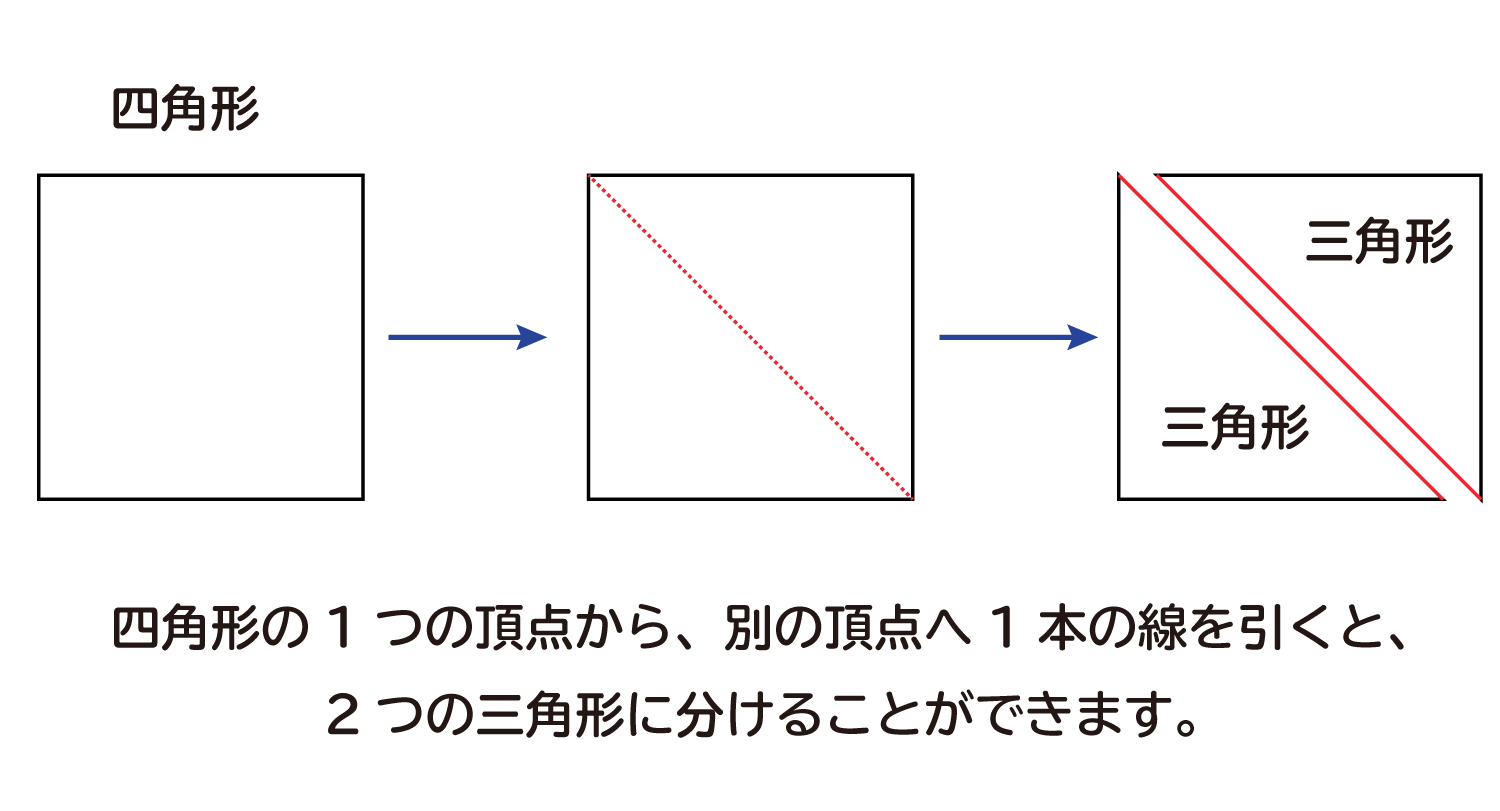



多角形の内角の和 は何度なのか を説明します おかわりドリル




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学
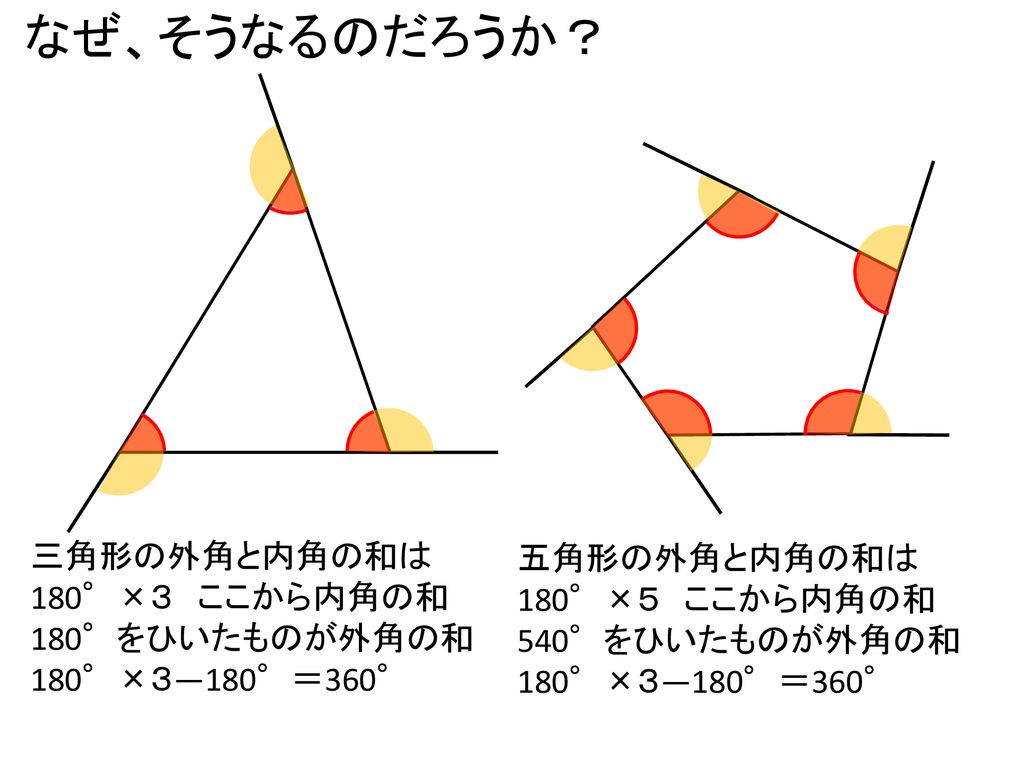



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download



内角の和 算数用語集



0 件のコメント:
コメントを投稿