22/2/18 千の位までの概数にするには1つ下の百の位を四捨五入します。 なので、百の位の数がポイントです。 つまり、答えは以上未満となります。 未満はその数を含まないという意味を持つので、に限りなく違いみたい数字になる感じですね。⑿ 四捨五入で千の位までの概数 にすると10万になる整数 概数 四捨五入の範囲⑴ 整数 14 解答 1 ⑴ 15以上24以下 ⑵ 35以上44以下 ⑶ 55以上64以下 ⑷ 5以上14以下 ⑸ 85以上94以下 ⑹ 95以上104以下 ⑺ 105注目する桁が ~ 0 ~ 4 なら切り捨て、 ~ 5 ~ 9 なら切り上げる方法です。 例えば、 を千の位に注目して四捨五入すると、 になります。

四捨五入の意味とやり方
千の位までの概数 四捨五入
千の位までの概数 四捨五入-13/6/17 概数の求め方 ~四捨五入~ 四捨五入とは、必要とされる数字よりも小さい部分に注目して、どちらに近いのかを判断することによって概数を導く方法を指します。 本問の場合、千の位までが必要とされていることから、それよりも一つ小さい百の位の数字にがい数四捨五入する位|算数|教科質問ひろば|進研ゼミ小学講座 百の位までの概数=上から3ケタまでの概数なので,十の位以下は切り捨て,切り上げ,四捨五入のいずれかになります。 したがって,の4以下を処理すればいいんです。




概数 およその数 切り捨て 切り上げのやり方 小学生 中学生の勉強
四捨五入の位 問題では「一万の位で四捨五入」や「千の位まで四捨五入」、「上から1けたまでの概数」という書かれ方をよくします。この時、四捨五入をする位が少し違ってきます。 例えば、「一万の位で四捨五入」の「で」の場合、その位(ここでは27/4/16 四捨五入と概数、子供に理解させるやり方は? 賢斗が4年生の時に苦労したのが四捨五入と概数だった。 という問題の時は、千の位のひとつ下の百の位に印をつけることが重要です。 このように、百の位の5の下に 印をつけます。 千の位までの概数が分かります。 などの問題の時、すごく分かりやすいです。 上から4けたの数字の下に 印をつけます⑼ 千の位を四捨五入すると7万になる数 ⑽ 四捨五入で千の位までの概数にするとになる数
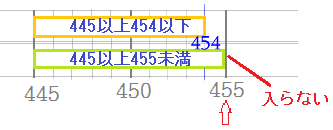
② 四捨五入して800 になるいちばん大きい整数は 何ですか。 ③ 四捨五入して百の位までのがい数にしたとき,800 に なる数のはんいを,以 い 上 じょう ,未 み 満 まん を使って表しましょう。 2 四捨五入して百の位までのがい数にしたとき,2800 に1 四捨五入をして,千の位までのがい数にしましょう。 (1)人(鳥取県の人口) 答え 人 (2)人(千葉県の人口) 答え 人 (3)人(東京都の人口) 答え 人19/2/21 \(\) を千の位で切り上げて、 \(\) 答え: \(\color{red}{}\) (3) \(\) を小数第 \(3\) 位で四捨五入して、 \(2748\) 答え: \(\color{red}{2748}\)
参考 さんこう までに、について四捨五入すると以下のようになります。 について、万の位までの概数:000;23/1/ 答え 〈切り捨て〉 〈切り上げ〉 一万の位までの概数にするときには千の位以下、千の位までの概数にするときには百の位以下というように、切り捨て・切り上げをするときには求める位よりも下の位の数字に注意しましょう。 スポンサードリンク⑴ 次の数を,千の位で四捨五入しなさい。 ① ② ⑵ 次の数を,四捨五入して,一万の位までのがい数にしなさい。 ① ② ⑶ 7以上10以下の整数を全部書きなさい。 ⑷ 2以上5未満の整数を全部書きなさい。



大きい数 概数 に関するq A Yahoo 知恵袋




小4概数教え方 千の位まで 上から1桁 約 全部 まで でいい
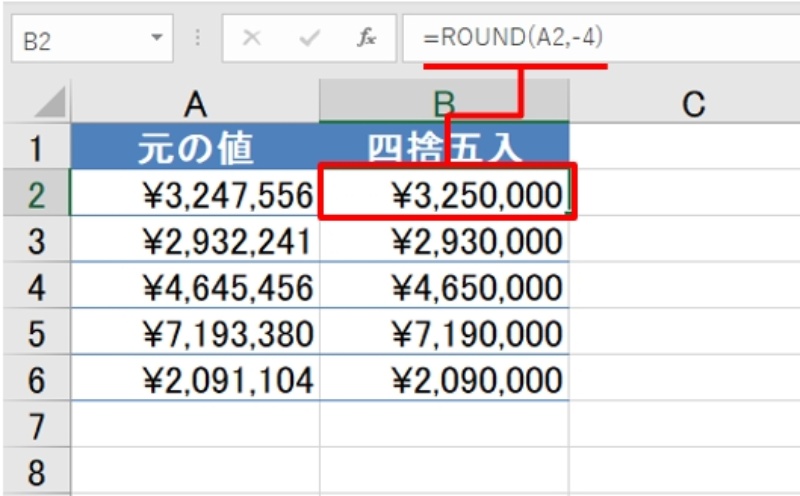
四捨五入して小数第2位までにする Dim value As Decimal = D Dim result As Decimal = Math Round(value, 2, MidpointRounding AwayFromZero)25/2/18 四捨五入して、〜の位までの概数を求める問題 練習5 次の数を四捨五入して、( )の位までのがい数にしなさい。 (1) 229(千) (2) (百) (3) (一万) (4) (一万) (5) (百万) (6) (十万)14/1/21 10分の1の位まで なので 1 00分の1の位 で四捨五入します。 概数とは「おおよその数で表す」という意味。 「商は四捨五入して、上から2桁の概数で求めなさい」なら、その3桁目の数字を四捨五入するが、のような小数は左の0を桁として数えない。




4年算数概数とその計算 1 教え方



S Kanbe
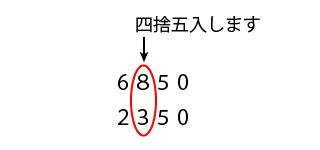
四捨五入して,千の位までのがい数にすると,3000になる 整数は、いくつからいくつまででしょう。 四捨五入して3000になる整数は 以上 以下です。 四捨五入して3000になる整数は 以上 未満です。 (1) (2) (3)四捨五入して1000になる整数は 1 2この仕方を四捨五入といいますね。 0、1、2、3、4のときは切り捨て、5、6、7、8、9のときは切り上げる! 次の数を四捨五入で、千の位までの概数にせよ。 例題① 2268m 例題② g ここが重要!! 概数で表すには、そのすぐ下の位の数字に注目する!千の位までの概数にするので,百の位で四捨五入します。 がいすう 6 なおひささんは,1470円の本と930円の本を買おうとしています。全部でお よそいくらになるか百の位で四捨五入し,がい数にして見積もりましょう。




四捨五入の意味とやり方



算数の宿題で分からないところがありました 1 四捨五入して百の位までの Yahoo 知恵袋
19/8/21 切り上げ概数の問題んんですけど (1)6073を切り上げて千の位の概数にするのと (2)を切り上げて万の位の概数にすると答えは何になる 四捨五入で10/1の位までの概数・・ 四捨五入で10/1の位までの概数のとき685と2 千の位で四捨五入できた。 数式は「=ROUND (, 4)」で、引数「桁数」を負の数で指定するのがポイント知 ・四捨五入して求めた概数の表す数範囲について理解できる。 ・用語「以上」、「以下」、「未満」の意味と使い方が分かる。 (2)単元の指導観 児童はこれまでに、大きな数として、億や兆の位までの命数法や加法・減法を学習している。このよう




1 Lihat Cara Penyelesaian Di Qanda




小4概数教え方 千の位まで 上から1桁 約 全部 まで でいい
問題 ①四捨五入で、一万のくらいまでの概数にせよ。 ②四捨五入で百の位までの概数にした時、3400になる整数のうち一番小さい数と一番大きい数を出せ。 ③1つの重さが384gのジャムがあります、このジャム215個分の重さはおおよそ何グラムになるか、上から1けたの概数にして答えを四捨五入指導の留意点 (1) どれを用いるか判断する 用いる場に応じて,3つの処理の仕方のどれを用いたらよいかを,自主的に判断できるようにすることが最も重要です ①切り上げた方がよいときの場面例 買い物の場面旅行費用準備 c 2275 は百の位を四捨五入して,約00といえるね c 約何万四捨五入して上から( )けたの概数にしましょう。 ① 3763(百の位まで) ( ) ② 1365(千の位まで) ( ) ③ 6019(百の位まで) ( ) ④ 1093(千の位まで) ( ) ⑤ 7769(千の位まで) ( ) ⑥ 9546(百の位まで) ( ) ⑦ 2738(千の位まで)




解決済み まで教えてください W やり方忘れました Clear




小4概数教え方 千の位まで 上から1桁 約 全部 まで でいい
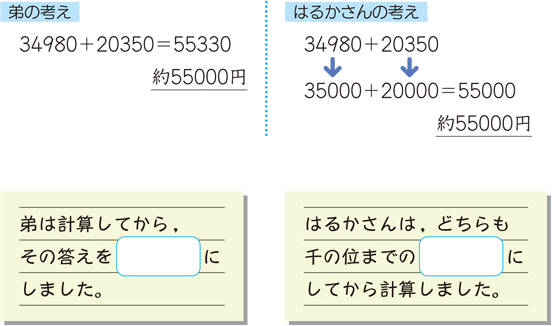
千の位までの概数にするには,百の位を四捨五入すればよいから, し し や ご に ゆ う くつの代金2450円 → 00円 服の代金 6735円 → 7000円 よって,買い物の合計は, 00+7000=9000 答え 9000円 概算は,計算の前に概数にしてから計算します。 trs511tmpjtd3 0 0 0 0一万 千 百 十 一2 0 0 0 0 →000 2 1 0 0 0 →000 2 2 0 0 0 →000 2 3 0 0 0 →000 2 4 0 0 0 →0002 4 9 9 9 →000 2 5 0 0 0 → 626/4/18 四捨五入のやり方 もとめる位の1つ下の位の数を見ます。 (例えば四捨五入をしての位までの概数を求めるときには1000の位を、1000の位までの概数にするときには100の位の数を見ます。) その数が 4・3・2・1・0のときには、切り捨て
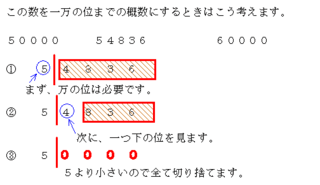



一万までの概数の まで とは Totoroの小道



楽しい授業って 考える楽しさを目指して 教師の毎日の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
千の位までの概数→四捨五入は百の位で行う。 ①切り上げてとなるのは、千の位が9である時で切り上がることを考慮すると、 9500以上となる。 ②切り捨ててとなるは、代となり、百の位で切り下がるのは4であるため、また、「千の位を四捨五入して概数を求めなさい」と問われたときは、求められる通りに千の位を四捨五入します、従って答えは万の位の概数となります。 例)千の位を四捨五入して、以下の数字の概数を求めなさい。 35 269 千の位の「5」を四捨五入すると答えはとなります。~の位までの概数にする場合は、そのひとつ下の位を四捨五入する 百の位の数は「7」なので、切り上げられます。 よって、32,718 を四捨五入して、千の位までの概数にした結果は、33,000 となります。 四捨五入して、上から~桁の概数にする




小数のわり算 小数第一位までのがい数で表す Youtube



Q Tbn And9gcsvjpqic S0pib8stjvzxd8ldzzn27cgnyhfv2mqaog4qkmhnny Usqp Cau
このしかたを四捨五入 ししゃごにゅう といいます。 ・がい数には,つぎのような2通りの表し方があります。 ある位までのがい数 例 →(千の位までのがい数) 上から1けたや2けたのがい数☆ 四捨五入して、()内のけたのがい数で表しましょう。 ① ⇒ 答 ② (上から3けた) ⇒ 答 ③ 答 四捨五入して 千 ④ (上から2けた) ⇒ 答 ⑤ 答 の位までのがい数にしたとき、 ⇒ ⇒ ⇒ ⇒ (千万の位) (千の位) (一億の位)「46 万と47 万の間の数で,千の位の数字が5,6,7,8,9 のときは47 万として,4,3,2,1 のときは46 万とする。このような仕方を四捨五入という。」 ↓ 「3249 を四捨五入して万の位まで求めるのに,9 を四捨五入してとし,これを四捨五入して とする。




小4算数 概数ってどんな時に使うの 範囲を求める問題はどうやって解けばいいの 疑問にお答えします ぴこスタ




商は四捨五入して上から2けたの概数で求めましょうとは イコプリメ 不登校経験をした小学生と母親の子育てブログ
7/8/18 四捨五入は、概数を求めるときにある位の0〜4までの数値を切り捨て、59の時は切り上げるというルールのことです。 算数の四捨五入問題ではつぎのような問題が出されます。 次の数字の百の位を四捨五入して、千の位までの概数にしましょう。 ①25 ②3510次の数を四捨五入して千の位までのがい数にしなさい。 (1) 4500 (2) 4499 (3) 6500 (4) 6499 (5) (6) 次の数を四捨五入して一万の位までのがい数にしなさい。 (7) (8) (9) (10) 647 (11) 8456 (12)「 の位までのがい数」も「上から けたのがい数」も、どちらも「 の位まで」「上から けた」の1つ下の位を四捨五入します。 求める位の右横に、縦線をひくとわかりやすいです。 3145を四捨五入してがい数にする例で説明します。 ・千の位までのがい数にする。 318 | 245 → ※「千の位まで」の「1つ下の位」の2を四捨五入する。




一万までの概数の まで とは Totoroの小道



1



Www Pref Okayama Jp Uploaded Life Misc Pdf




Ppt タイトル 四捨五入をしよう 千の位まで5 学年 4 年 教科 算数 活動イメージ 都道府県の面積を千の位までの概数であらわす 作成者 清久 利和 兵庫県たつの市立揖保小学校 Powerpoint Presentation Id




四捨五入の意味とやり方




切り上げ と 四捨五入 の意味の違いと使い方の例文 例文買取センター



四捨五入と概数 子供に理解させるやり方は きれいの秘密を見つけよう 楽天ブログ




Ppt タイトル 四捨五入をしよう 千の位まで5 学年 4 年 教科 算数 活動イメージ 都道府県の面積を千の位までの概数であらわす 作成者 清久 利和 兵庫県たつの市立揖保小学校 Powerpoint Presentation Id




小4概数教え方 千の位まで 上から1桁 約 全部 まで でいい




四捨五入して 千の位までのがい数にすると になる整数のはんい 小学校 教えて Goo




の位までのがい数で表す Youtube




四捨五入の意味とやり方




1 Lihat Cara Penyelesaian Di Qanda




四捨五入して 上から1桁 2桁 の概数 にするやり方 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



Http Sansu Info Print Pdf 1 08 Gaisu Hanni1 Pdf




四捨五入の考え方 おおよその数 概数を使った小学算数の計算 リョースケ大学




四捨五入の意味とやり方




概数って何 大人もやり方がわからないのに小学生へ教える方法



Www Pref Kanagawa Jp Documents Pdf




小4 概数 およその数 切り捨て 切り上げ 四捨五入 Youtube




四捨五入の意味とやり方




算数 小4 32 およその数 がい数 Youtube



Http Www Edu Tens Net Syohp Murehp Kyuukou Purinto Pridata 4nen 4san9 Pdf




概数 およその数 切り捨て 切り上げのやり方 小学生 中学生の勉強



3




Ppt タイトル 四捨五入をしよう 千の位まで5 学年 4 年 教科 算数 活動イメージ 都道府県の面積を千の位までの概数であらわす 作成者 清久 利和 兵庫県たつの市立揖保小学校 Powerpoint Presentation Id




動画追加 第15回 数の大小 4年生 日能研の歩き方




プリントあり 概数になる範囲を出す問題 四捨五入すると になる整数 の範囲と最大最小の求め方 プリントあり そうちゃ式 分かりやすい図解算数 別館




Sqrt4 6ooo Descubre Como Resolverlo En Qanda




Square Descubre Como Resolverlo En Qanda



4年算数概数とその計算 1 教え方




家庭学習 次男小4 概数 1 息子達よ 個性派で行け




商は四捨五入して上から2けたの概数で求めましょうとは イコプリメ 不登校経験をした小学生と母親の子育てブログ




概数 およその数 切り捨て 切り上げのやり方 小学生 中学生の勉強




小学4年生の算数 がい数 大きな数のがい数 練習問題プリント ちびむすドリル 小学生




概数 がい数 とは 意味や計算問題 四捨五入など の復習 受験辞典




四捨五入1 4 中学受験 算数 小4レベル Youtube




概数の問題はこれで完璧 概数の求め方と注意点




この問題の解き方を詳しく教えてください Clear



教えてください 四捨五入して百の位までがい数にすると 3 Yahoo 知恵袋




小4概数教え方 千の位まで 上から1桁 約 全部 まで でいい




四捨五入の意味とやり方



小6算数 5年の振り返りです 商は四捨五入して小数第一位までの概数で求 Yahoo 知恵袋




超簡単 上から2桁の概数 がいすう で表す 小学校算数 5年生 Yattoke 小 中学生の学習サイト




Square Descubre Como Resolverlo En Qanda




がい数と四捨五入 Youtube




4年 がい数 ゲンタの授業ポートフォリオ




概数



Excelで 概数 にまるめる 関数使って四捨五入や切り捨てを簡単に 日経クロステック Xtech



四捨五入の問題の の中の位までのがい数の意味が分かりません Yahoo 知恵袋




概数 およその数 切り捨て 切り上げのやり方 小学生 中学生の勉強



ドリルズ 小学4年生 算数 の無料学習プリント算数 がい数



2



Sansu Info Print Pdf 1 08 Gaisu Kiriage Hani Pdf




小4 概数 およその数 切り捨て 切り上げ 四捨五入 Youtube



W8jxbwb3erwa Com Archives




およその数 四捨五入 Youtube




小4概数教え方 千の位まで 上から1桁 約 全部 まで でいい
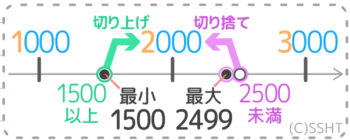



プリントあり 概数になる範囲を出す問題 四捨五入すると になる整数 の範囲と最大最小の求め方 プリントあり そうちゃ式 分かりやすい図解算数 別館
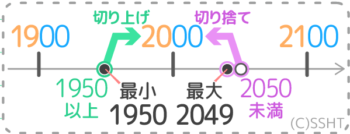



プリントあり 概数になる範囲を出す問題 四捨五入すると になる整数 の範囲と最大最小の求め方 プリントあり そうちゃ式 分かりやすい図解算数 別館



概数 おおよその数 ふるやまんの算数塾




がい数の練習問題の自主学習ノート 家庭学習レシピ



を四捨五入 切り上げ 切り捨てで千の位までの概数に Yahoo 知恵袋




商は四捨五入して上から2けたの概数で求めましょうとは イコプリメ 不登校経験をした小学生と母親の子育てブログ




動画で学習 11 がい数とその計算 その1 算数



がい数のドリル



概算と和 差の見積もり 算数用語集




分かりません 教えて下さい Clear




四捨五入の意味とやり方



Http Www Edu C Pref Miyagi Jp Tangen Math Ele4 Math Comment 14step Pdf



小学4年がい数 今習っている算数さっぱり分からんよ いざ突入 Extend



1




小学高学年 算数 自由自在問題集 基礎からできる日常学習と入試対策 小学高学年自由自在問題集 Shoi Gaku Kyoi Iku Kenkyui Kai Amazon Com Books




がい数の練習問題の自主学習ノート 家庭学習レシピ



Happylilac Net Gaisuans Matome Pdf
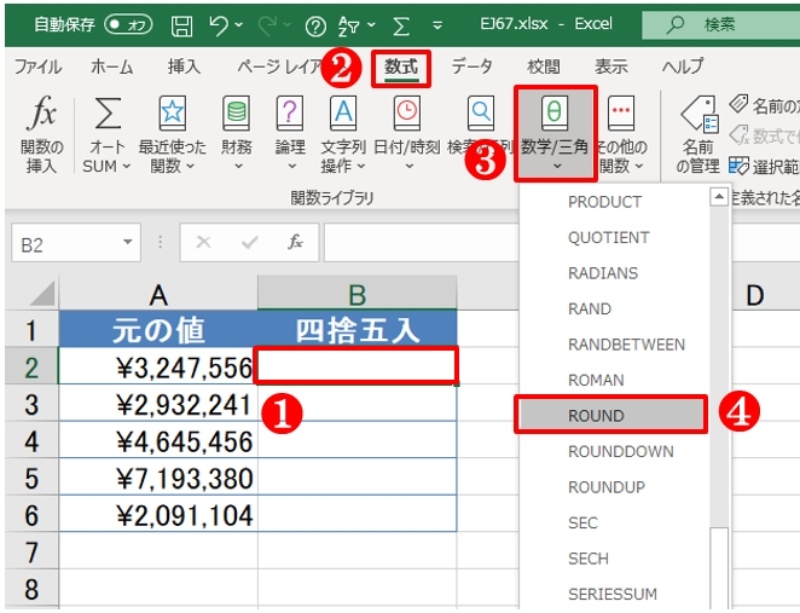



Excelで 概数 にまるめる 関数使って四捨五入や切り捨てを簡単に 日経クロステック Xtech




概数



Www Shinko Keirin Co Jp Keirinkan Sho Sansu Support Keyseat Data Sansu 4nen2 03 Pdf
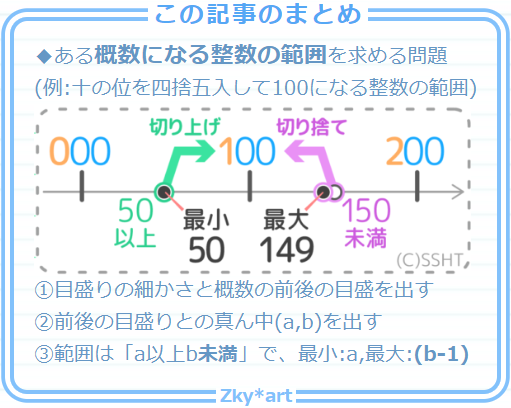



プリントあり 概数になる範囲を出す問題 四捨五入すると になる整数 の範囲と最大最小の求め方 プリントあり そうちゃ式 分かりやすい図解算数 別館



四捨五入して千のくらいまでの概数にすると 次の数になる整数の範囲を Yahoo 知恵袋




四捨五入の考え方 おおよその数 概数を使った小学算数の計算 リョースケ大学




小数 整数の筆算 がい数で答える Youtube



がい数 がい算 もう一度やり直しの算数 数学




一万までの概数の まで とは Totoroの小道




指定した桁で四捨五入する Round関数 Officeのチカラ




がい数を求めるときの四捨五入 小学生の算数質問ひろば 進研ゼミ小学講座



概数 がい数 とは 意味や計算問題 四捨五入など の復習 受験辞典




一万までの概数の まで とは Totoroの小道



0 件のコメント:
コメントを投稿